Question

（08年龍巖一中沖刺理）（12分）

如圖，四棱錐P―ABCD的底面ABCD是正方形，側棱PD⊥底面ABCD，PD=DC，E是PC的中點．

  （1）證明PA//平面BDE；

  （2）求二面角B―DE―C的大小；

  （3）在棱PB上是否存在點F，使PB⊥平面DEF？證明你的結論．

Answer 1

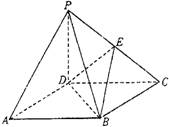
解析：解法一：（1）連結AC，設AC與BD交于O點，連結EO.

由底面ABCD是正方形知O為AC的中點，又E為PC的中點，

∴OE//PA，  ∵OE平面BDE，平面BDE，

∴PA//平面BDE   ………………4分

（2）∵PD⊥底面ABCD，∴PD⊥BC，又BC⊥CD，

∴BC⊥平面PCD，又PD=DC，E為PC的中點，

∴DE⊥PC，從而由三垂線定理知DE⊥BE，

∴∠BEC是二面角B―DE―C的平面角.

設正方形ABCD的邊長為a，

則，

在Rt△BCE中，

∴二面角B―DE―C的大小為 …………8分

（3）作EF⊥PB于點F，則Rt△PEF∽Rt△PBC，∴

∴PF?PB=PE?PC=，連結DF

∵在△PBD中，∠PDB=90°，PF?PB=a²=PD²， ∴PB⊥DF，

從而PB⊥平面DEF，此時

即在棱PB上存在點F，，使得PB⊥平面DEF  …………12分

解法二：（1）以D為坐標原點，分別以DA、DC、DP所在直線為x軸、y軸、z軸建立空間直角坐標系，設PD=DC=2，則A（2，0，0），P（0，0，2），E（0，1，1），

B（2，2，0）   

設 是平面BDE的一個法向量，

則由 

∵ ……4分