
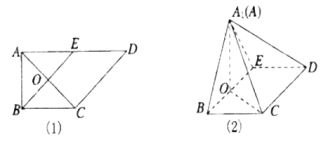
【題目】如圖(1)所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 與
與![]() 的交點.將△
的交點.將△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,如圖(2)所示.
的位置,如圖(2)所示.
(1)證明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)由圖(1)可得![]() ,由圖(2)可得
,由圖(2)可得![]() 平面
平面![]() ,根據(jù)線面垂直的性質(zhì)可得
,根據(jù)線面垂直的性質(zhì)可得![]() 平面
平面![]() ;(2)由平面
;(2)由平面![]() 平面
平面![]() 可得
可得![]() 為二面角
為二面角![]() 的平面角,所以
的平面角,所以![]() ,因此以
,因此以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系,分別求出平面
軸建立空間直角坐標(biāo)系,分別求出平面![]() 與平面
與平面![]() 的法向量,根據(jù)向量的夾角公式求解.
的法向量,根據(jù)向量的夾角公式求解.
試題解析:(1)證明:在圖(1)中,因為![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,
![]() ,所以
,所以![]() ,
,![]() ,
,
在圖(2)中,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
從而![]() 平面
平面![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() .
.
(2)由已知,平面![]() 平面
平面![]() ,
,
又由(1)知,![]() ,
,![]() ,
,
所以![]() 為二面角
為二面角![]() 的平面角,
的平面角,
所以![]() ,
,
如圖,以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標(biāo)系,
軸建立空間直角坐標(biāo)系,
因為![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,![]() .
.
設(shè)平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 與平面
與平面![]() 的夾角為
的夾角為![]() ,
,
則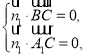 得
得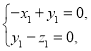 取
取![]() ;
;
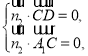 得
得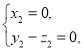 取
取![]() ;
;
從而![]() ,
,
即平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知圓
中,已知圓![]() 過坐標(biāo)原點
過坐標(biāo)原點![]() 且圓心在曲線
且圓心在曲線![]() 上.
上.
(1)若圓![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() 、
、![]() (不同于原點
(不同于原點![]() ),求證:
),求證:![]() 的面積為定值;
的面積為定值;
(2)設(shè)直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() ,求圓
,求圓![]() 的方程;
的方程;
(3)設(shè)直線![]() 與(2)中所求圓
與(2)中所求圓![]() 交于點
交于點![]() 、
、![]() ,
, ![]() 為直線
為直線![]() 上的動點,直線
上的動點,直線![]() ,
,![]() 與圓
與圓![]() 的另一個交點分別為
的另一個交點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 在直線
在直線![]() 異側(cè),求證:直線
異側(cè),求證:直線![]() 過定點,并求出定點坐標(biāo).
過定點,并求出定點坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知中國某手機(jī)品牌公司生產(chǎn)某款手機(jī)的年固定成本為40萬元,每生產(chǎn)1萬部還需另投入16萬元.設(shè)公司一年內(nèi)共生產(chǎn)該款手機(jī)![]() 萬部并全部銷量完,每萬部的銷售收入為
萬部并全部銷量完,每萬部的銷售收入為![]() 萬元,且
萬元,且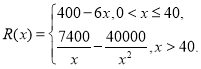
(1)寫出年利潤![]() 萬元關(guān)于年產(chǎn)量
萬元關(guān)于年產(chǎn)量![]() (萬部)的函數(shù)解析式;
(萬部)的函數(shù)解析式;
(2)當(dāng)年產(chǎn)量為多少萬部時,公司在該款手機(jī)的生產(chǎn)中所獲得的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期為π.
(Ⅰ)求f(![]() )的值;
)的值;
(Ⅱ)求函數(shù)f(x)的單調(diào)遞增區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某服裝商場為了了解毛衣的月銷售量y(件)與月平均氣溫x(℃)之間的關(guān)系,隨機(jī)統(tǒng)計了某4個月的月銷售量與當(dāng)月平均氣溫,其數(shù)據(jù)如下表:

(1) 算出線性回歸方程![]() ; (a,b精確到十分位)
; (a,b精確到十分位)
(2)氣象部門預(yù)測下個月的平均氣溫約為3℃,據(jù)此估計,求該商場下個月毛衣的銷售量.
(參考公式: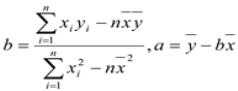 )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)據(jù)x1,x2,x3,…,xn是普通職工n(n≥3,n∈N*)個人的年收入,設(shè)這n個數(shù)據(jù)的中位數(shù)為x,平均數(shù)為y,方差為z,如果再加上世界首富的年收入xn+1,則這n+1個數(shù)據(jù)中,下列說法正確的是
A. 年收入平均數(shù)大大增大,中位數(shù)一定變大,方差可能不變
B. 年收入平均數(shù)大大增大,中位數(shù)可能不變,方差變大
C. 年收入平均數(shù)大大增大,中位數(shù)可能不變,方差也不變
D. 年收入平均數(shù)可能不變,中位數(shù)可能不變,方差可能不變
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com