
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)消去參數(shù)![]() 可以求出直線
可以求出直線![]() 的普通方程,由
的普通方程,由![]() ,
,![]() ,能求出曲線
,能求出曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)動點坐標(biāo),利用點到直線距離公式和三角函數(shù)的輔助角公式,確定距離![]() 的取值范圍.
的取值范圍.
詳解:解:(1)消去參數(shù)![]() 整理得,直線
整理得,直線![]() 的普通方程為:
的普通方程為:![]() ;
;
將![]() ,
,![]() ,代入曲線
,代入曲線![]() 的極坐標(biāo)方程
的極坐標(biāo)方程![]() .
.
曲線的直角坐標(biāo)方程為![]()
(2)設(shè)點![]()
![]() ,
,
則![]()
所以![]() 的取值范圍是
的取值范圍是![]() .
.
分析:本題考查參數(shù)方程化普通方程,極坐標(biāo)方程化直角坐標(biāo)方程,同時考查圓上的一點到直線距離的最值,直線與圓相離情況下,也可以通過圓心到直線距離![]() 與半徑
與半徑![]() 的關(guān)系表示,即距離最大值
的關(guān)系表示,即距離最大值![]() ,距離最小值
,距離最小值![]() .
.


 一線名師權(quán)威作業(yè)本系列答案
一線名師權(quán)威作業(yè)本系列答案科目:高中數(shù)學(xué) 來源: 題型:
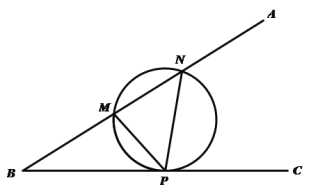
【題目】米勒問題,是指德國數(shù)學(xué)家米勒1471年向諾德爾教授提出的有趣問題:在地球表面的什么部位,一根垂直的懸桿呈現(xiàn)最長(即可見角最大?)米勒問題的數(shù)學(xué)模型如下:如圖,設(shè)![]() 是銳角
是銳角![]() 的一邊
的一邊![]() 上的兩定點,點
上的兩定點,點![]() 是邊
是邊![]() 邊上的一動點,則當(dāng)且僅當(dāng)
邊上的一動點,則當(dāng)且僅當(dāng)![]() 的外接圓與邊
的外接圓與邊![]() 相切時,
相切時,![]() 最大.若
最大.若![]() ,點
,點![]() 在
在![]() 軸上,則當(dāng)
軸上,則當(dāng)![]() 最大時,點
最大時,點![]() 的坐標(biāo)為( )
的坐標(biāo)為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】高考改革是教育體制改革中的重點領(lǐng)域和關(guān)鍵環(huán)節(jié),全社會極其關(guān)注.近年來,在新高考改革中,打破文理分科的“![]() ”模式初露端倪.其中“
”模式初露端倪.其中“![]() ”指必考科目語文、數(shù)學(xué)、外語,“
”指必考科目語文、數(shù)學(xué)、外語,“![]() ”指考生根據(jù)本人興趣特長和擬報考學(xué)校及專業(yè)的要求,從物理、化學(xué)、生物、歷史、政治、地理六科中選擇
”指考生根據(jù)本人興趣特長和擬報考學(xué)校及專業(yè)的要求,從物理、化學(xué)、生物、歷史、政治、地理六科中選擇![]() 門作為選考科目,其中語、數(shù)、外三門課各占
門作為選考科目,其中語、數(shù)、外三門課各占![]() 分,選考科目成績采用“賦分制”,即原始分?jǐn)?shù)不直接用,而是按照學(xué)生分?jǐn)?shù)在本科目考試的排名來劃分等級并以此打分得到最后得分.假定
分,選考科目成績采用“賦分制”,即原始分?jǐn)?shù)不直接用,而是按照學(xué)生分?jǐn)?shù)在本科目考試的排名來劃分等級并以此打分得到最后得分.假定![]() 省規(guī)定:選考科目按考生成績從高到低排列,按照占總體
省規(guī)定:選考科目按考生成績從高到低排列,按照占總體![]() 的,以此賦分
的,以此賦分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分.為了讓學(xué)生們體驗“賦分制”計算成績的方法,
分.為了讓學(xué)生們體驗“賦分制”計算成績的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)舉行了以此摸底考試(選考科目全考,單科全班排名,每名學(xué)生選三科計算成績),已知這次摸底考試中的物理成績(滿分
人)舉行了以此摸底考試(選考科目全考,單科全班排名,每名學(xué)生選三科計算成績),已知這次摸底考試中的物理成績(滿分![]() 分)頻率分布直方圖,化學(xué)成績(滿分
分)頻率分布直方圖,化學(xué)成績(滿分![]() 分)莖葉圖如下圖所示,小明同學(xué)在這次考試中物理
分)莖葉圖如下圖所示,小明同學(xué)在這次考試中物理![]() 分,化學(xué)
分,化學(xué)![]() 多分.
多分.

(1)求小明物理成績的最后得分;
(2)若小明的化學(xué)成績最后得分為![]() 分,求小明的原始成績的可能值;
分,求小明的原始成績的可能值;
(3)若小明必選物理,其他兩科在剩下的五科中任選,求小明此次考試選考科目包括化學(xué)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】盒中裝有![]() 個零件,其中
個零件,其中![]() 個是使用過的,另外
個是使用過的,另外![]() 個未經(jīng)使用.
個未經(jīng)使用.
(1)從盒中每次隨機抽取![]() 個零件,每次觀察后都將零件放回盒中,求
個零件,每次觀察后都將零件放回盒中,求![]() 次抽取中恰有
次抽取中恰有![]() 次抽到使用過的零件的概率;
次抽到使用過的零件的概率;
(2)從盒中隨機抽取![]() 個零件,使用后放回盒中,記此時盒中使用過的零件個數(shù)為
個零件,使用后放回盒中,記此時盒中使用過的零件個數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=excosx﹣x.(13分)
(1)求曲線y=f(x)在點(0,f(0))處的切線方程;
(2)求函數(shù)f(x)在區(qū)間[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax2﹣ax﹣xlnx,且f(x)≥0.
(Ⅰ)求a;
(Ⅱ)證明:f(x)存在唯一的極大值點x0 , 且e﹣2<f(x0)<2﹣2 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
已知在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() ,(
,(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點![]() 是曲線
是曲線![]() 上的一個動點,求它到直線
上的一個動點,求它到直線![]() 的距離
的距離![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A. 兩個變量的相關(guān)關(guān)系一定是線性相關(guān)
B. 兩個隨機變量的線性相關(guān)線越強,則相關(guān)系數(shù)的絕對值就越接近于0
C. 在回歸直線方程![]() 中,當(dāng)解釋變量
中,當(dāng)解釋變量![]() 每增加1個單位時,預(yù)報變量
每增加1個單位時,預(yù)報變量![]() 平均增加1個單位
平均增加1個單位
D. 對分類變量![]() 與
與![]() ,隨機變量
,隨機變量![]() 的觀測值
的觀測值![]() 越大,則判斷“
越大,則判斷“![]() 與
與![]() 有關(guān)系”的把握程度越大
有關(guān)系”的把握程度越大
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com