【題目】已知函數f（x）=loga（1﹣x）+loga（x+3）（0＜a＜1）
（1）求函數f（x）的定義域；
（2）求函數f（x）的零點；
（3）若函數f（x）的最小值為﹣4，求a的值．
【答案】
（1）解：要使函數有意義：則有 
，解之得：﹣3＜x＜1，
則函數的定義域為：（﹣3，1）
（2）解：函數可化為f（x）=loga（1﹣x）（x+3）=loga（﹣x2﹣2x+3）
由f（x）=0，得﹣x2﹣2x+3=1，
即x2+2x﹣2=0， 
∵ 
，∴函數f（x）的零點是 
（3）解：函數可化為：
f（x）=loga（1﹣x）（x+3）=loga（﹣x2﹣2x+3）=loga[﹣（x+1）2+4]
∵﹣3＜x＜1，∴0＜﹣（x+1）2+4≤4，
∵0＜a＜1，∴loga[﹣（x+1）2+4]≥loga4，
即f（x）min=loga4，由loga4=﹣4，得a﹣4=4，
∴ 
【解析】（1）根據對數的真數大于零，列出不等式組并求出解集，函數的定義域用集合或區間表示出來；（2）利用對數的運算性質對解析式進行化簡，再由f（x）=0，即﹣x2﹣2x+3=1，求此方程的根并驗證是否在函數的定義域內；（3）把函數解析式化簡后，利用配方求真數在定義域內的范圍，再根據對數函數在定義域內遞減，求出函數的最小值loga4，得loga4=﹣4利用對數的定義求出a的值．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，橢圓： 
的離心率為
，直線l：y＝2上的點和橢圓上的點的距離的最小值為1．
(Ⅰ) 求橢圓的方程；
(Ⅱ) 已知橢圓的上頂點為A，點B，C是上的不同于A的兩點，且點B，C關于原點對稱，直線AB，AC分別交直線l于點E，F．記直線
與
的斜率分別為
， 
．
① 求證： 
為定值；
② 求△CEF的面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）＝|x－1|＋|2x－1|．
（Ⅰ）若對
x＞0，不等式f（x）≥tx恒成立，求實數t的最大值M；
（Ⅱ）在（Ⅰ）成立的條件下，正實數a，b滿足a2＋b2＝2M．證明：a＋b≥2ab．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，過橢圓
： 
的左右焦點
分別作直線
， 
交橢圓于
與
，且
.
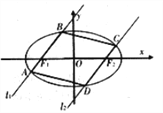
（1）求證：當直線
的斜率
與直線
的斜率
都存在時， 
為定值；
（2）求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市為了制定合理的節電方案，供電局對居民用電進行了調查，通過抽樣，獲得了某年200戶居民每戶的月均用電量（單位：度），將數據按照
， 
， 
， 
， 
， 
， 
， 
， 
分成9組，制成了如圖所示的頻率分布直方圖．
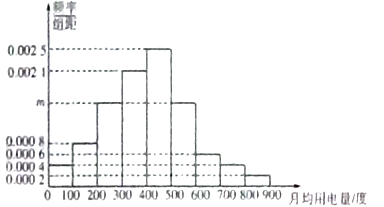
（Ⅰ）求直方圖中
的值并估計居民月均用電量的中位數；
（Ⅱ）現從第8組和第9組的居民中任選取2戶居民進行訪問，則兩組中各有一戶被選中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
=（2cos
， 
sin
），
=（cos
，2cos
），（ω＞0），設函數f（x）=
，且f（x）的最小正周期為π．
（1）求函數f（x）的表達式；
（2）求f（x）的單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩企業生產同一種型號零件，按規定該型號零件的質量指標值落在
內為優質品.從兩個企業生產的零件中各隨機抽出了500件，測量這些零件的質量指標值，得結果如下表：
甲企業：
乙企業：
（1）已知甲企業的500件零件質量指標值的樣本方差
，該企業生產的零件質量指標值
服從正態分布
，其中
近似為質量指標值的樣本平均數
（注：求
時，同一組數據用該區間的中點值作代表），
近似為樣本方差
，試根據該企業的抽樣數據，估計所生產的零件中，質量指標值不低于71.92的產品的概率.（精確到0.001）
（2）由以上統計數據完成下面
列聯表，并問能否在犯錯誤的概率不超過0.01的前提下，認為“兩個分廠生產的零件的質量有差異”.
附注：
參考數據： 
，
參考公式： 
， 
，
.
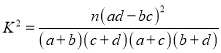
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
