【題目】下列函數中，在區間（﹣1， 
）上單調遞減的函數為（ ）
A.y=x2
B.y=3x﹣1
C.y=log2（x+1）
D.y=﹣sinx
53隨堂測系列答案科目：高中數學 來源： 題型：
【題目】設
是空間兩條直線， 
是空間兩個平面，則下列命題中不正確的是（ ）
A. 當
時，“
”是“
”的充要條件
B. 當
時，“
”是“
”的充分不必要條件
C. 當
時，“
”是“
”的必要不充分條件
D. 當
時，“
”是“
”的充分不必要條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4—4：坐標系與參數方程]以平面直角坐標系原點為極點，x軸正半軸為極軸，建立極坐標系，兩種坐標系中取相同長度單位，已知曲線
的參數方程為
，（ 
為參數，且
），曲線
的極坐標方程為
(1)求
的極坐標方程與
的直角坐標方程；
(2))若P是
上任意一點，過點P的直線
交
于點M,N，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC的三個頂點A（m，n）、B（2，1）、C（﹣2，3）；
（1）求BC邊所在直線的方程；
（2）BC邊上中線AD的方程為2x﹣3y+6=0，且S△ABC=7，求點A的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的外接圓半徑R= 
，角A，B，C的對邊分別是a，b，c，且 
= 
（1）求角B和邊長b；
（2）求S△ABC的最大值及取得最大值時的a，c的值，并判斷此時三角形的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
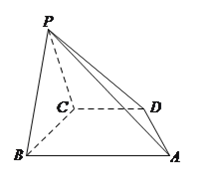
【題目】在四棱錐
中，底面
是直角梯形， 
， 
， 
，平面
平面
．
（Ⅰ）求證： 
平面
．
（Ⅱ）求平面
和平面
所成二面角（小于
）的大小．
（Ⅲ）在棱
上是否存在點
使得
平面
？若存在，求
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】張老師開車上班，有路線①與路線②兩條路線可供選擇. 路線①：沿途有
兩處獨立運行的交通信號燈，且兩處遇到綠燈的概率依次為
，若
處遇紅燈或黃燈，則導致延誤時間2分鐘；若
處遇紅燈或黃燈，則導致延誤時間3分鐘；若兩處都遇綠燈，則全程所花時間為20分鐘.
路線②：沿途有
兩處獨立運行的交通信號燈，且兩處遇到綠燈的概率依次為
，若
處遇紅燈或黃燈，則導致延誤時間8分鐘；若
處遇紅燈或黃燈，則導致延誤時間5分鐘；若兩處都遇綠燈，則全程所花時間為15分鐘.
（1）若張老師選擇路線①，求他20分鐘能到校的概率；
（2）為使張老師日常上班途中所花時間較少，你建議張老師選擇哪條路線？并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據下列算法語句，將輸出的A值依次記為a1 ， a2 ， …，an ， …，a2015；已知函數f（x）=a2sin（ωx+φ）（ω＞0，|φ|＜ 
）的最小正周期是a1 ， 且函數y=f（x）的圖象關于直線x= 
對稱．
（Ⅰ）求函數y=f（x）表達式；
（Ⅱ）已知△ABC中三邊a，b，c對應角A，B，C，a=4，b=4 
，∠A=30°，求f（B）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
