
【題目】已知雙曲線![]() 的焦點是橢圓
的焦點是橢圓![]() :
: ![]() 的頂點,
的頂點, ![]() 為橢圓
為橢圓![]() 的左焦點且橢圓
的左焦點且橢圓![]() 經過點
經過點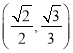 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右頂點作斜率為
的右頂點作斜率為![]() (
(![]() )的直線交橢圓
)的直線交橢圓![]() 于另一點
于另一點![]() ,連結
,連結![]() 并延長
并延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,當
,當![]() 的面積取得最大值時,求
的面積取得最大值時,求![]() 的面積.
的面積.
科目:高中數學 來源: 題型:
【題目】貴陽與凱里兩地相距約200千米,一輛貨車從貴陽勻速行駛到凱里,規定速度不得超過100千米![]() 時,已知貨車每小時的運輸成本
時,已知貨車每小時的運輸成本![]() 以元為單位
以元為單位![]() 由可變部分和固定部分組成:可變部分與速度
由可變部分和固定部分組成:可變部分與速度![]() 千米
千米![]() 時
時![]() 的平方成正比,比例系數為
的平方成正比,比例系數為![]() ;固定部分為64元.
;固定部分為64元.
![]() 把全程運輸成本
把全程運輸成本![]() 元
元![]() 表示為速度
表示為速度![]() 千米
千米![]() 時
時![]() 的函數,并指出這個函數的定義域;
的函數,并指出這個函數的定義域;
![]() 為了使全程運輸成本最小,貨車應以多大速度行駛?
為了使全程運輸成本最小,貨車應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】心理學家發現視覺和空間能力與性別有關,孝感市黃陂路高中數學興趣小組為了驗證這個結論,從興趣小組中抽取50名同學(男30女20),給所有同學幾何題和代數題各一題,讓各位同學自由選擇一道題進行解答.選題情況如下表:(單位:人)

(1)能否據此判斷有![]() 的把握認為視覺和空間能力與性別有關?
的把握認為視覺和空間能力與性別有關?
(2)以上列聯表中女生選做幾何題的頻率作為概率,從該校1500名女生中隨機選6名女生,記6名女生選做幾何題的人數為![]() ,求
,求![]() 的數學期望
的數學期望![]() 和方差
和方差![]() .
.
附表:

參考公式: 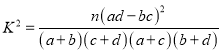 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知⊙H被直線x-y-1=0,x+y-3=0分成面積相等的四個部分,且截x軸所得線段的長為2。
(I)求⊙H的方程;
(Ⅱ)若存在過點P(0,b)的直線與⊙H相交于M,N兩點,且點M恰好是線段PN的中點,求實數b的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】水葫蘆原產于巴西,![]() 年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過
年作為觀賞植物引入中國. 現在南方一些水域水葫蘆已泛濫成災嚴重影響航道安全和水生動物生長. 某科研團隊在某水域放入一定量水葫蘆進行研究,發現其蔓延速度越來越快,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() ,經過
,經過![]() 個月其覆蓋面積為
個月其覆蓋面積為![]() . 現水葫蘆覆蓋面積
. 現水葫蘆覆蓋面積![]() (單位
(單位![]() )與經過時間
)與經過時間![]() 個月的關系有兩個函數模型
個月的關系有兩個函數模型![]() 與
與![]() 可供選擇.
可供選擇.
(參考數據:![]() )
)
(Ⅰ)試判斷哪個函數模型更合適,并求出該模型的解析式;
(Ⅱ)求原先投放的水葫蘆的面積并求約經過幾個月該水域中水葫蘆面積是當初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1(側棱垂直于底面的棱柱為直棱柱)中,BC=CC1=1,AC=2,∠ABC=90°. 
(1)求證:平面ABC1⊥平面A1B1C;
(2)設D為AC的中點,求平面ABC1與平面C1BD所成銳角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
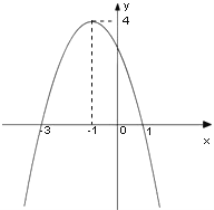
【題目】如圖是一個二次函數y=f(x)的圖象
(1)寫出這個二次函數的零點
(2)求這個二次函數的解析式
(3)當實數k在何范圍內變化時,函數g(x)=f(x)-kx在區間[-2,2]上是單調函數?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓中心為坐標原點O,對稱軸為坐標軸,且過M(2, ![]() ) ,N(
) ,N(![]() ,1)兩點,
,1)兩點,
(I)求橢圓的方程;
(II)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓C恒有兩個交點A,B,且![]() ?若存在,寫出該圓的方程,并求|AB |的取值范圍,若不存在說明理由。
?若存在,寫出該圓的方程,并求|AB |的取值范圍,若不存在說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com