
在 中,角
中,角 所對的邊分別是
所對的邊分別是 ,已知
,已知 .
.
(Ⅰ)若 的面積等于
的面積等于 ,求
,求 ;
;
(Ⅱ)若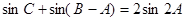 ,求
,求 的面積.
的面積.
(Ⅰ)2,2(Ⅱ)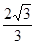
解析試題分析:(Ⅰ)由 ,運用余弦定理可得
,運用余弦定理可得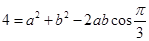 ,由
,由 的面積等于
的面積等于 ,運用三角形面積公式可得,
,運用三角形面積公式可得,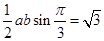 ,聯立即可解得
,聯立即可解得 ;(Ⅱ)利用三角形內角和定理先將
;(Ⅱ)利用三角形內角和定理先將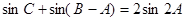 化為
化為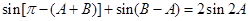 ,利用誘導公式及兩角和與差的正弦公式將上式化為
,利用誘導公式及兩角和與差的正弦公式將上式化為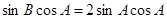 ,分兩種情況,若
,分兩種情況,若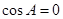 ,則求出A,B,C三角,利用解直角三角形求出
,則求出A,B,C三角,利用解直角三角形求出 ,從而求出面積,若
,從而求出面積,若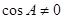 ,求出A,B關系,利用正弦定理求出
,求出A,B關系,利用正弦定理求出 關系,結合(Ⅰ)中結果
關系,結合(Ⅰ)中結果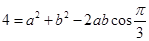 求出
求出 ,從而求出三角形面積.
,從而求出三角形面積.
試題解析:(Ⅰ)由余弦定理及已知條件得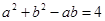
又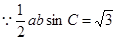 ,得
,得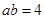 3分
3分
聯立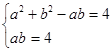 解得
解得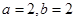 5分
5分
(Ⅱ)由題意得,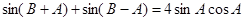
即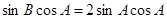 . 7分
. 7分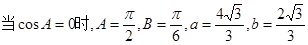
 的面積
的面積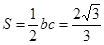 9分
9分
當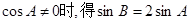 ,由正弦定理得
,由正弦定理得 ,
,
聯立方程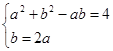
解得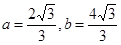
所以 的面積
的面積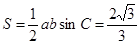 ,綜上,
,綜上, 的面積為
的面積為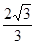 . 12分
. 12分
考點:正弦定理,余弦定理,三角形面積公式,三角變換,運算求解能力


 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:解答題
地面上有兩座塔AB、CD,相距120米,一人分別在兩塔底部測得一塔頂仰角為另一塔頂仰角的2倍,在兩塔底連線的中點O測得兩塔頂的仰角互為余角,求兩座塔的高度。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com