
【題目】已知定義在[0,1]上的函數f(x)滿足:
①f(0)=f(1)=0;
②對所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若對所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,則m的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:依題意,定義在[0,1]上的函數y=f(x)的斜率|k|< ![]() ,
,
依題意可設k>0,構造函數f(x)= 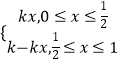 (0<k<
(0<k< ![]() ),滿足f(0)=f(1)=0,|f(x)﹣f(y)|<
),滿足f(0)=f(1)=0,|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
當x∈[0, ![]() ],且y∈[0,
],且y∈[0, ![]() ]時,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k|
]時,|f(x)﹣f(y)|=|kx﹣ky|=k|x﹣y|≤k| ![]() ﹣0|=k×
﹣0|=k× ![]() <
< ![]() ;
;
當x∈[0, ![]() ],且y∈[
],且y∈[ ![]() ,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+
,1],|f(x)﹣f(y)|=|kx﹣(k﹣ky)|=|k(x+y)﹣k|≤|k(1+ ![]() )﹣k|=
)﹣k|= ![]() <
< ![]() ;
;
當y∈[0, ![]() ],且x∈[
],且x∈[ ![]() ,1]時,同理可得,|f(x)﹣f(y)|<
,1]時,同理可得,|f(x)﹣f(y)|< ![]() ;
;
當x∈[ ![]() ,1],且y∈[
,1],且y∈[ ![]() ,1]時,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣
,1]時,|f(x)﹣f(y)|=|(k﹣kx)﹣(k﹣ky)|=k|x﹣y|≤k×(1﹣ ![]() )=
)= ![]() <
< ![]() ;
;
綜上所述,對所有x,y∈[0,1],|f(x)﹣f(y)|< ![]() ,
,
∵對所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,
∴m≥ ![]() ,即m的最小值為
,即m的最小值為 ![]() .
.
故選:B.
【考點精析】根據題目的已知條件,利用絕對值不等式的解法的相關知識可以得到問題的答案,需要掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】美索不達米亞平原是人類文明的發祥地之一.美索不達米亞人善于計算,他們創造了優良的計數系統,其中開平方算法是最具有代表性的.程序框圖如圖所示,若輸入a,n,ξ的值分別為8,2,0.5,(每次運算都精確到小數點后兩位)則輸出結果為( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣4:坐標系與參數方程):
在直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,已知射線θ= ![]() 與曲線
與曲線 ![]() (t為參數)相交于A,B來兩點,則線段AB的中點的直角坐標為 .
(t為參數)相交于A,B來兩點,則線段AB的中點的直角坐標為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知直線l的參數方程為 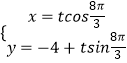 (t為參數),以坐標原點為極點,x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程為:ρ2﹣3ρ﹣4=0(ρ≥0).
(t為參數),以坐標原點為極點,x軸的正半軸為極軸,建立極坐標系,曲線C的極坐標方程為:ρ2﹣3ρ﹣4=0(ρ≥0).
(1)寫出直線l的普通方程與曲線C的直角坐標系方程;
(2)設直線l與曲線C相交于A,B兩點,求∠AOB的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐 ![]() 中,
中, ![]() 底面
底面 ![]() ,
, ![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,且
,且 ![]() ,
, ![]() 是
是 ![]() 的中點.
的中點.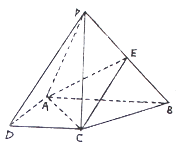
(1)求證:平面 ![]() 平面
平面 ![]() ;
;
(2)若二面角 ![]() 的余弦值為
的余弦值為 ![]() ,求直線
,求直線 ![]() 與平面
與平面 ![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生對函數![]() 的性質進行研究,得出如下的結論:
的性質進行研究,得出如下的結論:
①函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
②點![]() 是函數
是函數![]() 圖像的一個對稱中心;
圖像的一個對稱中心;
③存在常數![]() ,使
,使![]() 對一切實數
對一切實數![]() 均成立;
均成立;
④函數![]() 圖像關于直線
圖像關于直線![]() 對稱.其中正確的結論是__________.
對稱.其中正確的結論是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在正四棱柱 ![]() 中,
中, ![]() ,
, ![]() 分別為底面
分別為底面 ![]() 、底面
、底面 ![]() 的中心,
的中心, ![]() ,
, ![]() ,
, ![]() 為
為 ![]() 的中點,
的中點, ![]() 在
在 ![]() 上,且
上,且 ![]() .
.
(1)以 ![]() 為原點,分別以
為原點,分別以 ![]() ,
, ![]()
![]() 所在直線為
所在直線為 ![]() x 軸、
x 軸、 ![]() y 軸、
y 軸、 ![]() z 軸建立空間直角坐標系,求圖中各點的坐標.
z 軸建立空間直角坐標系,求圖中各點的坐標.
(2)以 ![]() D 為原點,分別以
D 為原點,分別以 ![]() , DC,DD1所在直線為
, DC,DD1所在直線為 ![]() 軸、
軸、 ![]() 軸、
軸、 ![]() 軸建立空間直角坐標系,求圖中各點的坐標.
軸建立空間直角坐標系,求圖中各點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com