
【題目】設函數f(x)=aexlnx+ ![]() ,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
,曲線y=f(x)在點(1,f(1))處得切線方程為y=e(x﹣1)+2.
(Ⅰ)求a、b;
(Ⅱ)證明:f(x)>1.
【答案】解:(Ⅰ)函數f(x)的定義域為(0,+∞),
f′(x)= ![]() +
+ ![]() ,
,
由題意可得f(1)=2,f′(1)=e,
故a=1,b=2;
(Ⅱ)由(Ⅰ)知,f(x)=exlnx+ ![]() ,
,
∵f(x)>1,∴exlnx+ ![]() >1,∴lnx>
>1,∴lnx> ![]() ﹣
﹣ ![]() ,
,
∴f(x)>1等價于xlnx>xe﹣x﹣ ![]() ,設函數g(x)=xlnx,則g′(x)=1+lnx,
,設函數g(x)=xlnx,則g′(x)=1+lnx,
∴當x∈(0, ![]() )時,g′(x)<0;當x∈(
)時,g′(x)<0;當x∈( ![]() ,+∞)時,g′(x)>0.
,+∞)時,g′(x)>0.
故g(x)在(0, ![]() )上單調遞減,在(
)上單調遞減,在( ![]() ,+∞)上單調遞增,從而g(x)在(0,+∞)上的最小值為g(
,+∞)上單調遞增,從而g(x)在(0,+∞)上的最小值為g( ![]() )=﹣
)=﹣ ![]() .
.
設函數h(x)=xe﹣x﹣ ![]() ,則h′(x)=e﹣x(1﹣x).
,則h′(x)=e﹣x(1﹣x).
∴當x∈(0,1)時,h′(x)>0;當x∈(1,+∞)時,h′(x)<0,
故h(x)在(0,1)上單調遞增,在(1,+∞)上單調遞減,
從而h(x)在(0,+∞)上的最大值為h(1)=﹣ ![]() .
.
綜上,當x>0時,g(x)>h(x),即f(x)>1.
【解析】(Ⅰ)求出定義域,導數f′(x),根據題意有f(1)=2,f′(1)=e,解出即可;(Ⅱ)由(Ⅰ)知,f(x)>1等價于xlnx>xe﹣x﹣ ![]() ,設函數g(x)=xlnx,函數h(x)=
,設函數g(x)=xlnx,函數h(x)= ![]() ,只需證明g(x)min>h(x)max,利用導數可分別求得g(x)min,h(x)max;
,只需證明g(x)min>h(x)max,利用導數可分別求得g(x)min,h(x)max;


科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限逼近圓的面積,并創立了“割圓術”.利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”.如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,其中n表示圓內接正多邊形的邊數,執行此算法輸出的圓周率的近似值依次為(參考數據: ![]() ≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
≈1.732,sin15°≈0.2588,sin75°≈0.1305)( ) 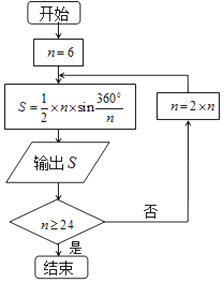
A.2.598,3,3.1048
B.2.598,3,3.1056
C.2.578,3,3.1069
D.2.588,3,3.1108
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數,且f(x+2)=f(x﹣2);當0≤x≤1時,f(x)= ![]() ,則f(1)+f(2)+f(3)+…+f等于( )
,則f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點與拋物線y2=4x的焦點F重合,且橢圓的離心率是
的右焦點與拋物線y2=4x的焦點F重合,且橢圓的離心率是 ![]() ,如圖所示.
,如圖所示.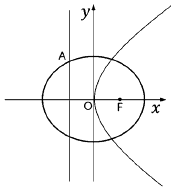
(1)求橢圓的標準方程;
(2)拋物線的準線與橢圓在第二象限相交于點A,過點A作拋物線的切線l,l與橢圓的另一個交點為B,求線段AB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f″(x)是y=f′(x)的導數.某同學經過探究發現,任意一個三次函數f(x)=ax3+bx2+cx+d(a≠0)都有對稱中心(x0 , f(x0)),其中x0滿足f″(x0)=0.已知函數f(x)= ![]() x3﹣
x3﹣ ![]() x2+3x﹣
x2+3x﹣ ![]() ,則f(
,則f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )= .
)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近期“共享單車”在全國多個城市持續升溫,某移動互聯網機構通過對使用者的調查得出,現在市場上常見的八個品牌的“共享單車”的滿意度指數如莖葉圖所示:
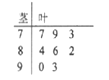
(Ⅰ)求出這組數據的平均數和中位數;
(Ⅱ)某用戶從滿意度指數超過80的品牌中隨機選擇兩個品牌使用,求所選兩個品牌的滿意度指數均超過85的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經國務院批復同意,鄭州成功入圍國家中心城市,某校學生團針對“鄭州的發展環境”對20名學生進行問卷調查打分(滿分100分),得到如圖1所示莖葉圖. 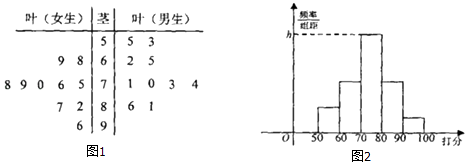
(Ⅰ)分別計算男生女生打分的平均分,并用數學特征評價男女生打分的數據分布情況;
(Ⅱ)如圖2按照打分區間[0,60)、[60,70)、[70,80)、[80,90)、[90,100]繪制的直方圖中,求最高矩形的高;
(Ⅲ)從打分在70分以下(不含70分)的同學中抽取3人,求有女生被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com