
【題目】已知函數(shù)![]() .
.
(1)求證:當(dāng)![]() 時(shí),對(duì)任意
時(shí),對(duì)任意![]() 恒成立;
恒成立;
(2)求函數(shù)![]() 的極值;
的極值;
(3)當(dāng)![]() 時(shí),若存在
時(shí),若存在![]() 且
且![]() ,滿足
,滿足![]() ,求證:
,求證:![]() .
.
【答案】(1)見(jiàn)解析 (2)極小值![]() ,無(wú)極大值. (3)見(jiàn)解析
,無(wú)極大值. (3)見(jiàn)解析
【解析】
(1)求導(dǎo)得到![]() ,即
,即![]() ,函數(shù)單調(diào)遞增,得到證明.
,函數(shù)單調(diào)遞增,得到證明.
(2)![]() ,討論
,討論![]() 和
和![]() 兩種情況,分別計(jì)算極值得到答案.
兩種情況,分別計(jì)算極值得到答案.
(3)![]() 在
在![]() 上為增函數(shù),當(dāng)
上為增函數(shù),當(dāng)![]() 時(shí)不成立,不防設(shè)
時(shí)不成立,不防設(shè)![]()
![]() ,計(jì)算得到
,計(jì)算得到![]() ,
,![]() 即證
即證![]() ,設(shè)
,設(shè)![]() ,只需證
,只需證![]() ,計(jì)算最值得到證明.
,計(jì)算最值得到證明.
(1)![]()
![]() ,
,![]() ,
,
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
所以當(dāng)![]() 時(shí),恒有
時(shí),恒有![]() 成立;
成立;
(2)由![]()
當(dāng)![]()
![]() 在
在![]() 上為增函數(shù),無(wú)極值
上為增函數(shù),無(wú)極值
當(dāng)![]()
![]() 在
在![]() 上為減函數(shù),在
上為減函數(shù),在![]() 上為增函數(shù),
上為增函數(shù),
![]() 有極小值
有極小值![]() ,無(wú)極大值,
,無(wú)極大值,
綜上知:當(dāng)![]() 無(wú)極值,
無(wú)極值,
當(dāng)![]() 有極小值
有極小值![]() ,無(wú)極大值.
,無(wú)極大值.
(3)當(dāng)![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
由(2)知,當(dāng)![]() ,
,![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
這時(shí),![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
所以不可能存在![]() ,
,
滿足![]() 且
且![]()
所以有![]()
現(xiàn)不防設(shè)![]() 得:
得:
![]()
![]() ①
①
![]()
![]() ②
②
由①②式可得:![]()
即![]()
又![]()
![]() ③
③
又要證![]() 即證
即證![]()
![]()
即證![]() ……④
……④
所以由③式知,只需證明:![]() 即證
即證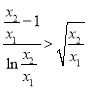
設(shè)![]() ,只需證
,只需證![]() ,即證:
,即證:![]()
令![]()
由 在
在![]() 上為增函數(shù),
上為增函數(shù),
![]()
![]() 成立,
成立,
所以由③知,![]() 成立,
成立,
所以![]() 成立.
成立.


 暑假作業(yè)海燕出版社系列答案
暑假作業(yè)海燕出版社系列答案 本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案
本土教輔贏在暑假高效假期總復(fù)習(xí)云南科技出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】規(guī)定投擲飛鏢3次為一輪,3次中至少兩次投中8環(huán)以上的為優(yōu)秀.現(xiàn)采用隨機(jī)模擬實(shí)驗(yàn)的方法估計(jì)某人投擲飛鏢的情況:先由計(jì)算器產(chǎn)生隨機(jī)數(shù)0或1,用0表示該次投鏢未在8環(huán)以上,用1表示該次投鏢在8環(huán)以上;再以每三個(gè)隨機(jī)數(shù)作為一組,代表一輪的結(jié)果.例如:“101”代表第一次投鏢在8環(huán)以上,第二次投鏢未在8環(huán)以上,第三次投鏢在8環(huán)以上,該結(jié)果代表這一輪投鏢為優(yōu)秀:"100”代表第一次投鏢在8環(huán)以上,第二次和第三次投鏢均未在8環(huán)以上,該結(jié)果代表這一輪投鏢為不優(yōu)秀.經(jīng)隨機(jī)模擬實(shí)驗(yàn)產(chǎn)生了如下10組隨機(jī)數(shù),據(jù)此估計(jì),該選手投擲飛鏢兩輪,至少有一輪可以拿到優(yōu)秀的概率是( )
101 | 111 | 011 | 101 | 010 | 100 | 100 | 011 | 111 | 001 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ax+blnx(a,b∈R)在點(diǎn)(1,f(1))處的切線方程為y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)當(dāng)x>1時(shí),f(x)![]() 0恒成立,求實(shí)數(shù)k的取值范圍;
0恒成立,求實(shí)數(shù)k的取值范圍;
(3)設(shè)g(x)=ex![]() x,求證:對(duì)于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求證:對(duì)于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)若不等式![]() 對(duì)
對(duì)![]() 恒成立,求
恒成立,求![]() 的值;
的值;
(2)若![]() 在
在![]() 內(nèi)有兩個(gè)極值點(diǎn),求負(fù)數(shù)
內(nèi)有兩個(gè)極值點(diǎn),求負(fù)數(shù)![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,
,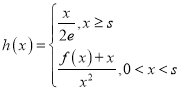 ,若對(duì)任意實(shí)數(shù)
,若對(duì)任意實(shí)數(shù)![]() ,總存在正實(shí)數(shù)
,總存在正實(shí)數(shù)![]() ,使得
,使得![]() 成立,求正實(shí)數(shù)
成立,求正實(shí)數(shù)![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 且在
且在![]() 上的最大值為
上的最大值為![]() ,
,
(1)求函數(shù)f(x)的解析式;
(2)判斷函數(shù)f(x)在(0,π)內(nèi)的零點(diǎn)個(gè)數(shù),并加以證明
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)![]() ,
,![]() 是兩條不同的直線,
是兩條不同的直線,![]() ,
,![]() ,
,![]() 是三個(gè)不同的平面,給出下列四個(gè)命題:
是三個(gè)不同的平面,給出下列四個(gè)命題:
①若![]() ,
,![]() ,則
,則![]()
②若![]() ,
,![]() ,
,![]() ,則
,則![]()
③若![]() ,
,![]() ,則
,則![]()
④若![]() ,
,![]() ,則
,則![]()
其中正確命題的序號(hào)是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,無(wú)窮數(shù)列
,無(wú)窮數(shù)列![]() 的首項(xiàng)
的首項(xiàng)![]() .
.
(1)如果![]() ,寫(xiě)出數(shù)列
,寫(xiě)出數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)如果![]() (
(![]() 且
且![]() ),要使得數(shù)列
),要使得數(shù)列![]() 是等差數(shù)列,求首項(xiàng)
是等差數(shù)列,求首項(xiàng)![]() 的取值范圍;
的取值范圍;
(3)如果![]() (
(![]() 且
且![]() ),求出數(shù)列
),求出數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com