【題目】設
，
是兩條不同的直線，
，
，
是三個不同的平面，給出下列四個命題：
①若
，
，則
②若
，
，，則
③若
，，則
④若
，
，則
其中正確命題的序號是（ ）
A.①和②B.②和③C.③和④D.①和④
【答案】A
【解析】
根據線面平行性質定理，結合線面垂直的定義，可得①是真命題；根據面面平行的性質結合線面垂直的性質，可得②是真命題；在正方體中舉出反例，可得平行于同一個平面的兩條直線不一定平行，垂直于同一個平面和兩個平面也不一定平行，可得③④不正確．由此可得本題的答案．
解：對于①，因為
，所以經過
作平面
，使
，可得
，
又因為
，
，所以
，結合得
．由此可得①是真命題；
對于②，因為
且
，所以
，結合，可得
，故②是真命題；
對于③，設直線
、是位于正方體上底面所在平面內的相交直線，
而平面
是正方體下底面所在的平面，
則有
且成立，但不能推出
，故③不正確；
對于④，設平面、、
是位于正方體經過同一個頂點的三個面，
則有
且
，但是
，推不出，故④不正確．
綜上所述，其中正確命題的序號是①和②
故選：
科目：高中數學 來源： 題型：
【題目】已知向量
=（2sinx，-1），
,函數f（x）=
．
（1）求函數f（x）的對稱中心；
（2）設△ABC的內角A，B，C所對的邊為a，b，c，且a2=bc，求f（A）的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市化工廠三個車間共有工人1000名，各車間男、女工人數如下表：已知在全廠工人中隨機抽取1名，抽到第二車間男工的可能性是0.15.
第一車間 | 第二車間 | 第三車間 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
(1)求x的值．
(2)現用分層抽樣的方法在全廠抽取50名工人，則應在第三車間抽取多少名工人？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
中，
，
（
且
）．
（1）求
的值；
（2）是否存在實數
，使得數列
為等差數列？若存在，求出的值；若不存在，請說明理由；
（3）設數列的前n項和為
，求．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體ABCDNPM中，底面ABCD是菱形，∠ABC＝60°，PA⊥平面ABCD，AB＝AP＝2，PM∥AB，PN∥AD，PM＝PN＝1.
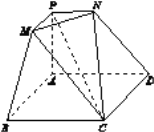
(1)求證：MN⊥PC；
(2)求平面MNC與平面APMB所成銳二面角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn，且Sn＝3an＋1(n∈N*).
(1)求數列{an}的通項公式；
(2)若數列{bn}滿足
，求數列{bn}的前n項和Tn.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
平面ABCD底面
是邊長為2的正方形， 
為
的中點，
為
的中點.
（1）求直線MN與直線CD所成角的余弦值；
（2）求直線OB與平面OCD所成的角.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
