
���}Ŀ���O(sh��)�E�A![]() �����x�E�A
�����x�E�A![]() �ġ����P(gu��n)�A�����̞�
�ġ����P(gu��n)�A�����̞�![]() �������タ
�������タ![]() �Ľ��c(di��n)�c�E�A
�Ľ��c(di��n)�c�E�A![]() ��һ�����c(di��n)�غϣ��ҙE�A
��һ�����c(di��n)�غϣ��ҙE�A![]() ���S��һ�����c(di��n)����ɂ����c(di��n)��(g��u)��ֱ�������Σ�
���S��һ�����c(di��n)����ɂ����c(di��n)��(g��u)��ֱ�������Σ�
(1)��E�A![]() �ķ��̺͡����P(gu��n)�A��
�ķ��̺͡����P(gu��n)�A��![]() �ķ��̣�
�ķ��̣�
(2)�^�����P(gu��n)�A��![]() ������һ�c(di��n)
������һ�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ���c(di��n)��
���c(di��n)��![]() ������(bi��o)ԭ�c(di��n)����
������(bi��o)ԭ�c(di��n)����![]() ���C��ԭ�c(di��n)
���C��ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x�Ƕ�ֵ������
�ľ��x�Ƕ�ֵ������![]() ��ȡֵ����.
��ȡֵ����.
���𰸡���1���E�A![]() �ķ��̞�
�ķ��̞�![]() �������P(gu��n)�A��
�������P(gu��n)�A��![]() �ķ��̞�
�ķ��̞�![]() ����2��
����2��![]() ��
��![]() .
.
��������
��1������֪�l��Ӌ����E�A![]() �ķ��̺͡����P(gu��n)�A��
�ķ��̺͡����P(gu��n)�A��![]() �ķ���
�ķ���
��2��ֱ���c�E�A�ཻ��(li��n)�����̽M����![]() ���
���![]() ֮�g�P(gu��n)ϵ��Ȼ���ٱ�ʾ���c(di��n)�����ľ��x��ʽ����������Y(ji��)��
֮�g�P(gu��n)ϵ��Ȼ���ٱ�ʾ���c(di��n)�����ľ��x��ʽ����������Y(ji��)��
�⣺��1����?y��n)������タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() �c�E�A
�c�E�A![]() ��һ�����c(di��n)�غϣ�����
��һ�����c(di��n)�غϣ�����![]() ������?y��n)�E�A
������?y��n)�E�A![]() ���S��һ�����c(di��n)����ɂ����c(di��n)��(g��u)��ֱ�������Σ�����
���S��һ�����c(di��n)����ɂ����c(di��n)��(g��u)��ֱ�������Σ�����![]() ��
��
�ʙE�A![]() �ķ��̞�
�ķ��̞�![]() �������P(gu��n)�A��
�������P(gu��n)�A��![]() �ķ��̞�
�ķ��̞�![]()
��2���O(sh��)![]() ��
��
(li��n)�����̽M ��
��![]() ��
��
![]() ��
��
��![]()
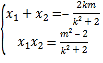 ��
��![]()
![]()
�ɗl��![]() ��
��![]() ,
,
����ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ��
��
��![]() ��
��![]() �鶨ֵ
�鶨ֵ
�ֈA�ĵ�ֱ��![]() �ľ��x��
�ľ��x��![]() ��ֱ��
��ֱ��![]() �c�A�й����c(di��n)
�c�A����c(di��n)![]() ���M��l��
���M��l��
��![]() ����
����![]() ����
����![]() ��
��![]()
��![]() ����
����![]() ������
������![]() ����
����![]() ��
��![]()
�C�ϣ�![]() ��
��![]()


 ȫ�ܾ�����ϵ�д�
ȫ�ܾ�����ϵ�д� һ�nһ���n�r�_(d��)��(bi��o)ϵ�д�
һ�nһ���n�r�_(d��)��(bi��o)ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪ƽ���τ��c(di��n)P�����c(di��n)![]() �ľ��x��P��ֱ��
�ľ��x��P��ֱ��![]() �ľ��x��1.ӛ���c(di��n)P��܉�E������C.
�ľ��x��1.ӛ���c(di��n)P��܉�E������C.
��1��������C�ķ��̣�
��2���^�c(di��n)![]() ��ֱ��
��ֱ��![]() ������C��A��B���c(di��n)���c(di��n)A�P(gu��n)��x�S�Č��Q�c(di��n)��D���C����ֱ��
������C��A��B���c(di��n)���c(di��n)A�P(gu��n)��x�S�Č��Q�c(di��n)��D���C����ֱ��![]() ���^�c(di��n)F.
���^�c(di��n)F.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���S��ָ����![]() ���Ї�(y��n)��ı����ԣ�ˇ�g(sh��)�ԣ����C�ԣ��N(y��n)�����S�������W(xu��)�rֵ.�@һ��ֵ�܉������˂������У����Q���ǽ�����ˇ�g(sh��)��������ı���.�҂����x����
���Ї�(y��n)��ı����ԣ�ˇ�g(sh��)�ԣ����C�ԣ��N(y��n)�����S�������W(xu��)�rֵ.�@һ��ֵ�܉������˂������У����Q���ǽ�����ˇ�g(sh��)��������ı���.�҂����x����![]() �ęE�A�Q�顰�S��E�A�����t�����ķN�f�������_�Ă���(sh��)�飨 ��
�ęE�A�Q�顰�S��E�A�����t�����ķN�f�������_�Ă���(sh��)�飨 ��
�ٙE�A![]() �ǡ��S��E�A��
�ǡ��S��E�A��
�����E�A![]() ��
��![]() ���ҽ��c(di��n)
���ҽ��c(di��n)![]() �ҝM��
�ҝM��![]() ���tԓ�E�A�顰�S��E�A����
���tԓ�E�A�顰�S��E�A����
���O(sh��)�E�A![]() ��
��![]() �����c(di��n)��F������c(di��n)��B������c(di��n)��A����
�����c(di��n)��F������c(di��n)��B������c(di��n)��A����![]() ���tԓ�E�A�顰�S��E�A����
���tԓ�E�A�顰�S��E�A����
���O(sh��)�E�A��![]() ��
��![]() ��������c(di��n)�քeA��B�����ҽ��c(di��n)�քe��
��������c(di��n)�քeA��B�����ҽ��c(di��n)�քe��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �ɵȱȔ�(sh��)�У��tԓ�E�A�顰�S��E�A����
�ɵȱȔ�(sh��)�У��tԓ�E�A�顰�S��E�A����
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() ��ʾ�������������е�9�K��,�F(xi��n)�ƶ��_���c�P(gu��n)����Ҏ(gu��)�t����:
��ʾ�������������е�9�K��,�F(xi��n)�ƶ��_���c�P(gu��n)����Ҏ(gu��)�t����:
(1)��һ�K���M(j��n)���_�����P(gu��n)��һ�ν���һ�β���;
(2)��![]() ���κ���r�¶������M(j��n)��һ�β���;�������
���κ���r�¶������M(j��n)��һ�β���;�������![]() ,Ҫ���
,Ҫ���![]() ����߅����ֻ����
����߅����ֻ����![]() ���_����B(t��i)�r�ſ��Ԍ���
���_����B(t��i)�r�ſ��Ԍ���![]() �M(j��n)��һ�β���.������П���̎���_����B(t��i),��ôҪ�џ�
�M(j��n)��һ�β���.������П���̎���_����B(t��i),��ôҪ�џ�![]() �P(gu��n)�]������Ҫ_____�β���;�������
�P(gu��n)�]������Ҫ_____�β���;�������![]() ��,����8�K����̎���_����B(t��i),��ôҪʹ���П����_��������Ҫ_____�β���.
��,����8�K����̎���_����B(t��i),��ôҪʹ���П����_��������Ҫ_____�β���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��(���x)��֪����(sh��)![]() ,�������_�Y(ji��)Փ����( )
,�������_�Y(ji��)Փ����( )
A.��(d��ng)![]() �r,����(sh��)
�r,����(sh��)![]() �����ֵ.
�����ֵ.
B.���������![]() ,����(sh��)
,����(sh��)![]() һ��������Сֵ.
һ��������Сֵ.
C.���������![]() ,����(sh��)
,����(sh��)![]() ��
��![]() �ϵ�������(sh��).
�ϵ�������(sh��).
D.���������![]() ,�����(sh��)
,�����(sh��)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��
��![]() ���x���ʞ�
���x���ʞ�![]() ���E�A
���E�A![]() ��
��![]() ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n)![]() .
.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)�c(di��n)![]() �ǙE�A
�ǙE�A![]() �ϵ�����һ�c(di��n)���侀
�ϵ�����һ�c(di��n)���侀![]() �c�E�A
�c�E�A![]() �����c(di��n)
�����c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c�E�A
�c�E�A![]() ����ֻ��һ�������c(di��n)��ֱ��
����ֻ��һ�������c(di��n)��ֱ��![]() �c�E�A
�c�E�A![]() ����
����![]() ��
��![]() �ɂ��ஐ�c(di��n)���C����
�ɂ��ஐ�c(di��n)���C����![]() ��e�鶨ֵ.
��e�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���҇��Ŵ���(sh��)�W(xu��)�������������g(sh��)������һ���������}�������(n��i)�ݞ飺������ԫ����ߣ�������������һ�ߣ�С��Ҳ��һ�ߣ��������Ա���С�����룮��������ꣿ�����Σ�����D�ij����DԴ���@���}Ŀ����(zh��)��ԓ�����D����ݔ��x=20���tݔ���ĽY(ji��)���飨������
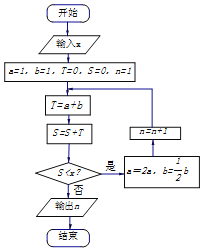
A. 3B. 4C. 5D. 6
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �����c(di��n)
�����c(di��n)![]() ��ֱ��
��ֱ��![]() �cy�S�����c(di��n)P.���c�E�A����A��B���c(di��n).A��E�A������c(di��n)��B��x�S�ϵ���Ӱǡ��
�cy�S�����c(di��n)P.���c�E�A����A��B���c(di��n).A��E�A������c(di��n)��B��x�S�ϵ���Ӱǡ��![]() ��
��
��1����E�AE�ķ��̣�
��2��M��E�AE�ڵ�һ��������һ�c(di��n)��ֱ��MP�c�E�A������һ�c(di��n)N����![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����߅�L��![]() ��������
��������![]() �،��Ǿ�
�،��Ǿ�![]() ����ʹ��ƽ��
����ʹ��ƽ��![]() ƽ��
ƽ��![]() ����������γɵ������F
����������γɵ������F![]() �У��o�������Ă����}����
�У��o�������Ă����}����![]() ���ڮ���ֱ��
���ڮ���ֱ��![]() �c
�c![]() ���ɵĽǞ�
���ɵĽǞ�![]() ���۶����
���۶����![]() ����ֵ��
����ֵ��![]() ���������F
���������F![]() ���w�e��
���w�e��![]() .�������_���}����̖��___________.�������������_���}����̖��
.�������_���}����̖��___________.�������������_���}����̖��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com