Question

【題目】閱讀與探究

人教A版《普通高中課程標準實驗教科書 數學4（必修）》在第一章的小結中寫到：

將角放在直角坐標系中討論不但使角的表示有了統一的方法，而且使我們能夠借助直角坐標系中的單位圓，建立角的變化與單位圓上點的變化之間的對應關系，從而用單位圓上點的縱坐標、橫坐標來表示圓心角的正弦函數、余弦函數.因此，正弦函數、余弦函數的基本性質與圓的幾何性質（主要是對稱性）之間存在著非常緊密的聯系.例如，和單位圓相關的“勾股定理”與同角三角函數的基本關系有內在的一致性；單位圓周長為與正弦函數、余弦函數的周期為是一致的；圓的各種對稱性與三角函數的奇偶性、誘導公式等也是一致的等等.因此，三角函數的研究過程能夠很好地體現數形結合思想.

依據上述材料，利用正切線可以討論研究得出正切函數的性質.

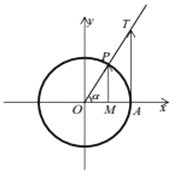
比如：由圖1.2-7可知，角的終邊落在四個象限時均存在正切線；角的終邊落在軸上時，其正切線縮為一個點，值為；角的終邊落在軸上時，其正切線不存在；所以正切函數的定義域是.

（1）請利用單位圓中的正切線研究得出正切函數的單調性和奇偶性；

（2）根據閱讀材料中途1.2-7，若角為銳角，求證： .

Answer 1

【答案】（1）見解析（2）見解析

【解析】試題分析：（1）在單位圓中畫出角的正切線，觀察隨增大正切線的值得變化情況，再觀察時，正切線的值隨增大時的變化情況，發現正切函數在區間上單調遞增.（2）當是銳角時，有，由此得到.

解析：（1）當時， 增大時正切線的值越來越大；當時，正切線與區間上的情況完全一樣；隨著角的終邊不停旋轉，正切線不停重復出現，故可得出正切函數在區間上單調遞增；由題意知正切函數的定義域關于原點對稱，在坐標系中畫出角 和，它們的終邊關于軸對稱，在單位圓中作出它們的正切線，可以發現它們的正切線長度相等，方向相反，即，得出正切函數為奇函數.

（2）如圖，當為銳角時，在單位圓中作出它的正弦線，正切線，又因為，所以，又 ，而，故即.