
【題目】在棱長均為![]() 的四面體
的四面體![]() 中,點(diǎn)
中,點(diǎn)![]() 為
為![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 為
為![]() 的中點(diǎn).若點(diǎn)
的中點(diǎn).若點(diǎn)![]() ,
,![]() 是平面
是平面![]() 內(nèi)的兩動點(diǎn),且
內(nèi)的兩動點(diǎn),且![]() ,
,![]() ,則
,則![]() 的面積為( )
的面積為( )
A. ![]() B. 3
B. 3
C. ![]() D. 2
D. 2
【答案】C
【解析】
建立空間直角坐標(biāo)系,寫出B,E,F的坐標(biāo),設(shè)M(x,y,0)的坐標(biāo),由![]() ,得出M的軌跡,同理得出N的軌跡,由
,得出M的軌跡,同理得出N的軌跡,由![]() ,即可得到
,即可得到![]() 的面積.
的面積.
建立空間直角坐標(biāo)系如圖所示,
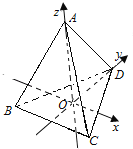
![]() ,底面
,底面![]() 為等邊三角形,且
為等邊三角形,且![]() .所以O(shè)D=2,B(-
.所以O(shè)D=2,B(-![]() ,-1,0),D(0,2,0),C(
,-1,0),D(0,2,0),C(![]() ,-1,0),點(diǎn)
,-1,0),點(diǎn)![]() 為
為![]() 的中點(diǎn),所以E(
的中點(diǎn),所以E(![]() ,
,![]() ,0),點(diǎn)
,0),點(diǎn)![]() 為
為![]() 的中點(diǎn),F(xiàn)(-
的中點(diǎn),F(xiàn)(-![]() ,-
,-![]() ,0),設(shè)M(x,y,0),
,0),設(shè)M(x,y,0),![]() ,
,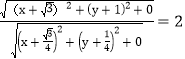 ,化簡得
,化簡得![]() ,且點(diǎn)M 是平面BCD 內(nèi)的動點(diǎn),所以點(diǎn)M在以(0,0)為圓心,以1為半徑的圓上,又
,且點(diǎn)M 是平面BCD 內(nèi)的動點(diǎn),所以點(diǎn)M在以(0,0)為圓心,以1為半徑的圓上,又![]() ,且點(diǎn)N 是平面BCD 內(nèi)的動點(diǎn),同理N也在這個圓上,且
,且點(diǎn)N 是平面BCD 內(nèi)的動點(diǎn),同理N也在這個圓上,且![]() ,所以MN為圓的直徑,因?yàn)锳O
,所以MN為圓的直徑,因?yàn)锳O![]() 面BCD,所以AO
面BCD,所以AO![]() MN,且AO=
MN,且AO=![]() ,
,![]() .
.
故選:C.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系xOy中,曲線C1的普通方程為![]() ,曲線C2參數(shù)方程為
,曲線C2參數(shù)方程為![]() 為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸,建立極坐標(biāo)系,直線l的極坐標(biāo)方程為
為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),以x軸正半軸為極軸,建立極坐標(biāo)系,直線l的極坐標(biāo)方程為![]() .
.
(1)求C1的參數(shù)方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知P是C2上參數(shù)![]() 對應(yīng)的點(diǎn),Q為C1上的點(diǎn),求PQ中點(diǎn)M到直線
對應(yīng)的點(diǎn),Q為C1上的點(diǎn),求PQ中點(diǎn)M到直線![]() 的距離取得最大值時,點(diǎn)Q的直角坐標(biāo).
的距離取得最大值時,點(diǎn)Q的直角坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 的右焦點(diǎn),點(diǎn)
的右焦點(diǎn),點(diǎn)![]() 在
在![]() 上,且
上,且![]() 軸.
軸.
(1)求![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 交
交![]() 于
于![]() 兩點(diǎn),交直線
兩點(diǎn),交直線![]() 于點(diǎn)
于點(diǎn)![]() .判定直線
.判定直線![]() 的斜率是否依次構(gòu)成等差數(shù)列?請說明理由.
的斜率是否依次構(gòu)成等差數(shù)列?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有極值
有極值![]() .
.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的極值;
的極值;
(3)若關(guān)于![]() 的方程
的方程![]() 有三個不同的實(shí)數(shù)解,求實(shí)數(shù)
有三個不同的實(shí)數(shù)解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙二人獨(dú)立破譯同一密碼,甲破譯密碼的概率為![]() ,乙破譯密碼的概率為
,乙破譯密碼的概率為![]() .記事件A:甲破譯密碼,事件B:乙破譯密碼.
.記事件A:甲破譯密碼,事件B:乙破譯密碼.
(1)求甲、乙二人都破譯密碼的概率;
(2)求恰有一人破譯密碼的概率;
(3)小明同學(xué)解答“求密碼被破譯的概率”的過程如下:
解:“密碼被破譯”也就是“甲、乙二人中至少有一人破譯密碼”所以隨機(jī)事件“密碼被破譯”可以表示為![]() 所以
所以![]()
請指出小明同學(xué)錯誤的原因?并給出正確解答過程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“中國大能手”是央視推出的一檔大型職業(yè)技能挑戰(zhàn)賽類節(jié)目,旨在通過該節(jié)目,在全社會傳播和弘揚(yáng)“勞動光榮、技能寶貴、創(chuàng)造偉大”的時代風(fēng)尚.某公司準(zhǔn)備派出選手代表公司參加“中國大能手”職業(yè)技能挑戰(zhàn)賽.經(jīng)過層層選拔,最后集中在甲、乙兩位選手在一項(xiàng)關(guān)鍵技能的區(qū)分上,選手完成該項(xiàng)挑戰(zhàn)的時間越少越好.已知這兩位選手在15次挑戰(zhàn)訓(xùn)練中,完成該項(xiàng)關(guān)鍵技能挑戰(zhàn)所用的時間![]() (單位:秒)及挑戰(zhàn)失敗(用“×”表示)的情況如下表1:
(單位:秒)及挑戰(zhàn)失敗(用“×”表示)的情況如下表1:
序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
| × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
據(jù)上表中的數(shù)據(jù),應(yīng)用統(tǒng)計軟件得下表2:
均值(單位:秒)方差 | 方差 | 線性回歸方程 | |
甲 | 85 | 50.2 |
|
乙 | 84 | 54 |
|
(1)根據(jù)上述回歸方程,預(yù)測甲、乙分別在下一次完成該項(xiàng)關(guān)鍵技能挑戰(zhàn)所用的時間;
(2)若該公司只有一個參賽名額,根據(jù)以上信息,判斷哪位選手代表公司參加職業(yè)技能挑戰(zhàn)賽更合適?請說明你的理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)如果函數(shù)![]() 在公共定義域D上,滿足
在公共定義域D上,滿足![]() ,那么就稱
,那么就稱![]() 為
為![]() 的“伴隨函數(shù)”.已知函數(shù)
的“伴隨函數(shù)”.已知函數(shù)![]() ,
,![]() .若在區(qū)間
.若在區(qū)間![]() 上,函數(shù)
上,函數(shù)![]() 是
是![]() 的“伴隨函數(shù)”,求實(shí)數(shù)
的“伴隨函數(shù)”,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,正實(shí)數(shù)
,正實(shí)數(shù)![]() 滿足
滿足![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 為常數(shù)).
為常數(shù)).
(Ⅰ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)是否存在正實(shí)數(shù)![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,若存在,求出實(shí)數(shù)
,若存在,求出實(shí)數(shù)![]() 的取值范圍;若不存在,請說明理由;
的取值范圍;若不存在,請說明理由;
(Ⅲ)當(dāng)![]() 時,
時, ![]() ,對
,對![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com