
����������ABC��A1B1C1�У�AB��AA1��D��E�քe����A1B1��AA1�����c(di��n)���c(di��n)F����AB�ϣ��� ��
��
��1�����C��EF��ƽ��BDC1��
��2�����C�� ƽ��
ƽ�� ��
��
�C��Ҋ����.
����ԇ�}��������1��Ҫ�C����ƽ�У�����Ҫ��ƽ��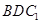 ��(n��i)��һ�lֱ���cֱ��
��(n��i)��һ�lֱ���cֱ��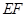 ƽ�У����}������������Ҫ�C����
ƽ�У����}������������Ҫ�C����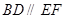 �����@��(g��)����߅��
�����@��(g��)����߅��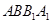 ��ֻҪȡ
��ֻҪȡ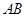 ���c(di��n)
���c(di��n)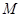 �����C��
�����C��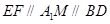 ���ã���2��Ҫ�C
���ã���2��Ҫ�C ƽ��
ƽ�� ������(j��)���洹ֱ���ж�����������Ҫ�C
������(j��)���洹ֱ���ж�����������Ҫ�C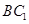 �cƽ��
�cƽ��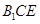 ��(n��i)�ăɗl�ֱཻ����ֱ���^����֪�l�������������Ă�(c��)���������Σ������
��(n��i)�ăɗl�ֱཻ����ֱ���^����֪�l�������������Ă�(c��)���������Σ������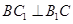 ������߀Ҫ��һ�l�����������
������߀Ҫ��һ�l�����������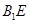 ��
�� ����һ�l��
����һ�l��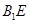 ��ƽ��
��ƽ��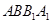 �У���ƽ���֪�R(sh��)��
�У���ƽ���֪�R(sh��)��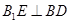 �������������������|(zh��)�ɵ�
�������������������|(zh��)�ɵ�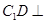 ƽ��
ƽ��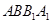 ���Ķ�
���Ķ�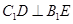 �������
�������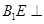 ƽ��
ƽ��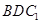 ������
������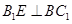 �����ǽY(ji��)Փ���C.
�����ǽY(ji��)Փ���C.
��1���C����ȡ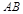 �����c(di��n)M����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/39/0/4x7ys.png" style="vertical-align:middle;" />������
�����c(di��n)M����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/39/0/4x7ys.png" style="vertical-align:middle;" />������ ��
��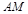 �����c(di��n)��
�����c(di��n)��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/22/e/y0lko1.png" style="vertical-align:middle;" />��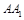 �����c(di��n)������
�����c(di��n)������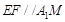 �� 2��
�� 2��
����������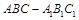 ��
�У�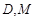 �քe��
�քe��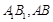 �����c(di��n)��
�����c(di��n)��
����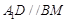 ����
����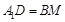 ���t��߅��A1DBM��ƽ����߅�Σ�
���t��߅��A1DBM��ƽ����߅�Σ�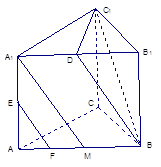
����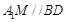 ������
������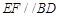 �� 5��
�� 5��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/e4/e/1utwi2.png" style="vertical-align:middle;" />ƽ��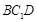 ��
��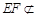 ƽ��
ƽ��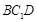 �����ԣ�
�����ԣ�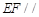 ƽ��
ƽ��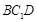 7��
7��
��2���B��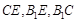 ����?y��n)��������?img src="http://thumb.zyjl.cn/pic5/tikupic/f0/e/1gok04.png" style="vertical-align:middle;" />��
����?y��n)��������?img src="http://thumb.zyjl.cn/pic5/tikupic/f0/e/1gok04.png" style="vertical-align:middle;" />��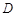 ��
��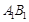 �����c(di��n)��
�����c(di��n)��
���ԣ�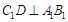 �����ԣ�����������ABC��A1B1C1�У�
�����ԣ�����������ABC��A1B1C1�У�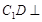 ��
��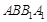 ��
��
���ԣ�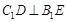 ����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/f2/4/dsalu1.png" style="vertical-align:middle;" />�����ԣ���߅��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/f2/4/dsalu1.png" style="vertical-align:middle;" />�����ԣ���߅��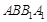 �������Σ���
�������Σ���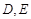 �քe��
�քe�� �����c(di��n)�����ԣ����C��
�����c(di��n)�����ԣ����C��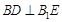 ��
��
���ԣ�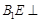 ��
��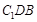 ����
����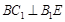 �� 11��
�� 11��
����?y��n)��������?img src="http://thumb.zyjl.cn/pic5/tikupic/40/8/1pnjb4.png" style="vertical-align:middle;" />��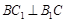 ������
������ ��
�� , 14��
, 14��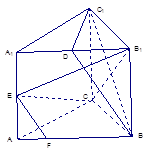


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D����֪һ�����FP��ABCD�ĵ�����߅�L(zh��ng)��1�������Σ��҂�(c��)��PC�͵���ABCD����PC��2��E�ǂ�(c��)��PC�ϵĄ�(d��ng)�c(di��n)
��1���������FP��ABCD���w�e��
��2���C����BD��AE��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��������ABC-A1B1C1�У��c(di��n)A1��ƽ��ABC��(n��i)����ӰD��AC�ϣ���ACB=90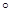 ��BC=1��AC=CC1=2.
��BC=1��AC=CC1=2.
(1)�C����AC1��A1B;
(2)�O(sh��)ֱ��AA1�cƽ��BCC1B1�ľ��x��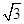 ��������A1-AB-C�Ĵ�С.
��������A1-AB-C�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
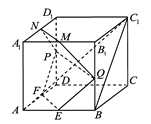
��D���������w ��
��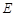 ��
��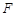 ��
��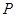 ��
��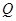 ��
�� ��
��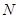 �քe����
�քe����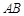 ��
��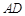 ��
�� ��
�� 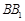 ��
��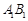 ��
��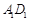 �����c(di��n).���C��
�����c(di��n).���C��
��1��ֱ��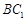 ��ƽ��
��ƽ��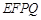 ��
��
��2��ֱ�� ��ƽ��
��ƽ��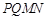 .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��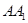 ��
�� ��A��
��A�� ��ĸ����
��ĸ���� �ǵ���A
�ǵ���A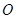 ��ֱ����
��ֱ����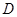 ��
��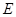 �քe��
�քe��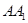 ��
��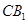 �����c(di��n)��
�����c(di��n)��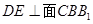 ��
��
��1���C���� ��
��
��2���C���� ��
��
��3�����O(sh��)�@�ǂ�(g��)���������Зl�w�e���Ժ��Բ�Ӌ(j��)��С�~��������������ط���߮������~�ε������F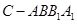 ��(n��i)��(hu��)�б�����Σ�U(xi��n)�����~�����ĸ���.
��(n��i)��(hu��)�б�����Σ�U(xi��n)�����~�����ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D�������F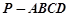 �ĵ���
�ĵ���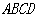 ��ƽ����߅�Σ�
��ƽ����߅�Σ�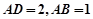 ��
��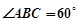 ��
�� ��
��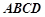 ���O(sh��)
���O(sh��)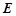 ��
��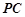 ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)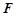 �ھ���
�ھ���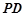 ����
����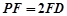 ��
��
��1�����C��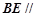 ƽ��
ƽ��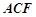 ��
��
��2���O(sh��)�����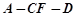 �Ĵ�С��
�Ĵ�С��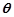 ����
����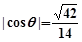 ����
����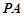 ���L(zh��ng)��
���L(zh��ng)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����D��ʾ�Ķ����wABCDE�У�AB��ƽ��ACD,DE��ƽ��ACD��AC=AD=CD=DE=2��AB=1��
��1��Ո(q��ng)?ji��n)ھ���CE���ҵ�һ�c(di��n)F��ʹ��ֱ��BF��ƽ��ACD�����C����
��2����ƽ��BCE�cƽ��ACD�����J����ǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����D��ʾ�Ď��w�У���߅��ABCD�ǵ������Σ�AB��CD����DAB= 60�㣬F(xi��n)C��ƽ��ABCD��AE��BD��CB=" CD=" CF��
��1�����C��BD��ƽ��AED��
��2��������F��BD��C������ֵ��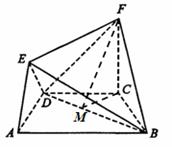
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��D��������ABCD��A1B1C1D1�ĵ���ABCD�������Σ�O��������ģ�A1O��ƽ��ABCD��AB��AA1��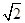 .
.
(1)�C����A1C��ƽ��BB1D1D��
(2)��ƽ��OCB1�cƽ��BB1D1D�ĊA�ǦȵĴ�С��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com