
【題目】十九大提出:堅決打贏脫貧攻堅戰(zhàn),做到精準扶貧.某縣積極引導農民種植一種名貴中藥材,從而大大提升了該縣村民的經濟收入.2019年年底,該機構從該縣種植的這種名貴藥材的農戶中隨機抽取了100戶,統(tǒng)計了他們2019年因種植,中藥材所獲純利潤(單位:萬元)的情況(假定農戶因種植中藥材這一項一年最多獲利11萬元),統(tǒng)計結果如下表所示:
![]()
(1)由表可以認為,該縣農戶種植中藥材所獲純利潤Z(單位:萬元)近似地服從正態(tài)分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() (每組數據取區(qū)間的中點值),
(每組數據取區(qū)間的中點值),![]() 近似為樣本方差
近似為樣本方差![]() .若該縣有1萬戶農戶種植了該中藥材,試估算所獲純利潤Z在區(qū)間(1.9,8.2)的戶數;
.若該縣有1萬戶農戶種植了該中藥材,試估算所獲純利潤Z在區(qū)間(1.9,8.2)的戶數;
(2)為答謝廣大農戶的積極參與,該調查機構針對參與調查的農戶舉行了抽獎活動,抽獎規(guī)則如下:在一箱子中放置5個除顏色外完全相同的小球,其中紅球1個,黑球4個.讓農戶從箱子中隨機取出一個小球,若取到紅球,則抽獎結束;若取到黑球,則將黑球放回箱中,讓他繼續(xù)取球,直到取到紅球為止(取球次數不超過10次).若農戶取到紅球,則視為中獎,獲得2000元的獎勵,若一直未取到紅球,則視為不中獎.現農戶張明參加了抽獎活動,記他中獎時取球的次數為隨機變量X,他取球的次數為隨機變量Y.
①證明:![]() 為等比數列;
為等比數列;
②求Y的數學期望.(精確到0.001)
參考數據:![]() .若隨機變量
.若隨機變量![]() 則
則![]()
![]() .
.
 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】袋子有5個不同的小球,編號分別為1,2,3,4,5,從袋中一次取出三個球,記隨機變量![]() 是取出球的最大編號與最小編號的差,數學期望為
是取出球的最大編號與最小編號的差,數學期望為![]() ,方差為
,方差為![]() 則下列選項正確的是( )
則下列選項正確的是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高鐵是我國國家名片之一,高鐵的修建凝聚著中國人的智慧與汗水.如圖所示,B、E、F為山腳兩側共線的三點,在山頂A處測得這三點的俯角分別為![]() 、
、![]() 、
、![]() ,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.
,計劃沿直線BF開通穿山隧道,現已測得BC、DE、EF三段線段的長度分別為3、1、2.

(1)求出線段AE的長度;
(2)求出隧道CD的長度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面問題中,若問題中的三角形存在,求
這三個條件中任選一個,補充在下面問題中,若問題中的三角形存在,求![]() 的值;若問題中的三角形不存在,說明理由.
的值;若問題中的三角形不存在,說明理由.
問題:是否存在![]() ,它的內角
,它的內角![]() 的對邊分別為
的對邊分別為![]() ,且
,且![]() ,
,![]() ,________?
,________?
注:如果選擇多個條件分別解答,按第一個解答計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】CES是世界上最大的消費電子技術展,也是全球最大的消費技術產業(yè)盛會.2020CES消費電子展于2020年1月7日—10日在美國拉斯維加斯舉辦.在這次CES消費電子展上,我國某企業(yè)發(fā)布了全球首款彩色水墨屏閱讀手機,驚艷了全場.若該公司從7名員工中選出3名員工負責接待工作(這3名員工的工作視為相同的工作),再選出2名員工分別在上午、下午講解該款手機性能,若其中甲和乙至多有1人負責接待工作,則不同的安排方案共有__________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為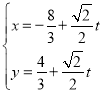 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() .
.
(Ⅰ)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在平面直角坐標系![]() 中,設直線
中,設直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.若點
兩點.若點![]() 恰為線段
恰為線段![]() 的三等分點,求
的三等分點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有
的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有![]() 成立,則稱此數列為“λ~k”數列.
成立,則稱此數列為“λ~k”數列.
(1)若等差數列![]() 是“λ~1”數列,求λ的值;
是“λ~1”數列,求λ的值;
(2)若數列![]() 是“
是“![]() ”數列,且an>0,求數列
”數列,且an>0,求數列![]() 的通項公式;
的通項公式;
(3)對于給定的λ,是否存在三個不同的數列![]() 為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com