
【題目】已知三棱錐P﹣ABC的所有棱長為1.M是底面△ABC內部一個動點(包括邊界),且M到三個側面PAB,PBC,PAC的距離h1,h2,h3成單調遞增的等差數列,記PM與AB,BC,AC所成的角分別為α,β,γ,則下列正確的是( )
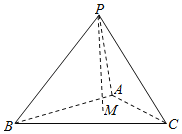
A.α=βB.β=γC.α<βD.β<γ
【答案】D
【解析】
PM與AB,BC,AC所成的角分別為α,β,γ,即比較OM與AB,BC,AC夾角的大小,然后在△ABC中解決問題, 由于d1<d2<d3,可知M在如圖陰影區域(不包括邊界)
從圖中可以看出,OM與BC所成角小于OM與AC所成角,即得解.
依題意知正四面體P﹣ABC的頂點P在底面ABC的射影是正三角形ABC的中心O,
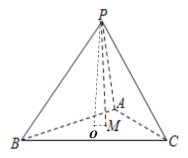
由余弦定理可知,
cosα=cos∠PMOcos<MO,AB>,其中<MO,AB>表示直線MO與AB的夾角,
同理可以將β,γ轉化,
cosβ=cos∠PMOcos<MO,BC>,其中<MO,BC>表示直線MO與BC的夾角,
cosγ=cos∠PMOcos<MO,AC>,其中<MO,AC>表示直線MO與AC的夾角,
由于∠PMO是公共的,因此題意即比較OM與AB,BC,AC夾角的大小,
設M到AB,BC,AC的距離為d1,d2,d3 則d1=sin![]() ,其中θ是正四面體相鄰兩個面所成角,sinθ
,其中θ是正四面體相鄰兩個面所成角,sinθ![]() ,
,
所以d1,d2,d3成單調遞增的等差數列,然后在△ABC中解決問題
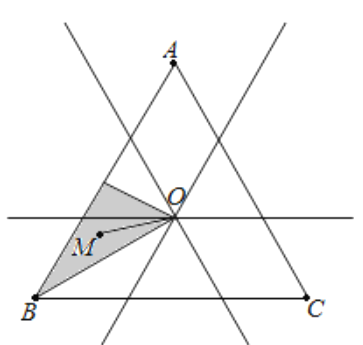
由于d1<d2<d3,可知M在如圖陰影區域(不包括邊界)
從圖中可以看出,OM與BC所成角小于OM與AC所成角,所以β<γ,
故選:D.


科目:高中數學 來源: 題型:
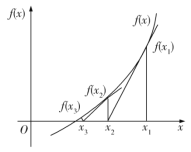
【題目】牛頓迭代法(Newton's method)又稱牛頓–拉夫遜方法(Newton–Raphsonmethod),是牛頓在17世紀提出的一種近似求方程根的方法.如圖,設![]() 是
是![]() 的根,選取
的根,選取![]() 作為
作為![]() 初始近似值,過點
初始近似值,過點![]() 作曲線
作曲線![]() 的切線
的切線![]() 與
與![]() 軸的交點的橫坐標
軸的交點的橫坐標![]() ,稱
,稱![]() 是
是![]() 的一次近似值,過點
的一次近似值,過點![]() 作曲線
作曲線![]() 的切線,則該切線與
的切線,則該切線與![]() 軸的交點的橫坐標為
軸的交點的橫坐標為![]() ,稱
,稱![]() 是
是![]() 的二次近似值.重復以上過程,直到
的二次近似值.重復以上過程,直到![]() 的近似值足夠小,即把
的近似值足夠小,即把![]() 作為
作為![]() 的近似解.設
的近似解.設![]() 構成數列
構成數列![]() .對于下列結論:
.對于下列結論:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() .
.
其中正確結論的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,離心率為
中,離心率為![]() 的橢圓
的橢圓![]() 的左頂點為
的左頂點為![]() ,過原點
,過原點![]() 的直線(與坐標軸不重合)與橢圓
的直線(與坐標軸不重合)與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于
軸交于![]() ,
, ![]() 兩點.若直線
兩點.若直線![]() 斜率為
斜率為 ![]() 時,
時, ![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)試問以![]() 為直徑的圓是否經過定點(與直線
為直徑的圓是否經過定點(與直線![]() 的斜率無關)?請證明你的結論.
的斜率無關)?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線Γ:y2=2px(p>0)的焦點為F,P是拋物線Γ上一點,且在第一象限,滿足![]() (2,2
(2,2![]() )
)
(1)求拋物線Γ的方程;
(2)已知經過點A(3,﹣2)的直線交拋物線Γ于M,N兩點,經過定點B(3,﹣6)和M的直線與拋物線Γ交于另一點L,問直線NL是否恒過定點,如果過定點,求出該定點,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大約在20世紀30年代,世界上許多國家都流傳著這樣一個題目:任取一個正整數![]() ,如果它是偶數,則除以2;如果它是奇數,則將它乘以3加1,這樣反復運算,最后結果必然是1.這個題目在東方被稱為“角谷猜想”,世界一流的大數學家都被其卷入其中,用盡了各種方法,甚至動用了最先進的電子計算機,驗算到對700億以內的自然數上述結論均為正確的,但卻給不出一般性的證明.例如取
,如果它是偶數,則除以2;如果它是奇數,則將它乘以3加1,這樣反復運算,最后結果必然是1.這個題目在東方被稱為“角谷猜想”,世界一流的大數學家都被其卷入其中,用盡了各種方法,甚至動用了最先進的電子計算機,驗算到對700億以內的自然數上述結論均為正確的,但卻給不出一般性的證明.例如取![]() ,則要想算出結果1,共需要經過的運算步數是( )
,則要想算出結果1,共需要經過的運算步數是( )
A.9B.10C.11D.12
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn,且![]() =9,S6=60.
=9,S6=60.
(I)求數列{an}的通項公式;
(II)若數列{bn}滿足bn+1﹣bn=![]() (n∈N+)且b1=3,求數列
(n∈N+)且b1=3,求數列![]() 的前n項和Tn.
的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,過點
中,過點![]() 的動圓恒與
的動圓恒與![]() 軸相切,
軸相切,![]() 為該圓的直徑,設點
為該圓的直徑,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的任意直線
的任意直線![]() 與曲線
與曲線![]() 交于點
交于點![]() ,
,![]() 為
為![]() 的中點,過點
的中點,過點![]() 作
作![]() 軸的平行線交曲線
軸的平行線交曲線![]() 于點
于點![]() ,
,![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,除
,除![]() 以外,直線
以外,直線![]() 與
與![]() 是否有其它公共點?說明理由.
是否有其它公共點?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com