
【題目】某中學有初中學生1800人,高中學生1200人.為了解學生本學期課外閱讀時間,現(xiàn)采用分層抽樣的方法,從中抽取了100名學生,先統(tǒng)計了他們課外閱讀時間,然后按“初中學生”和“高中學生”分為兩組,再將每組學生的閱讀時間(單位:小時)分為5組:[0,10),[10,20),[20,30),[30,40),[40,50],并分別加以統(tǒng)計,得到如下圖所示的頻率分布直方圖.

(I)寫出a的值;
(II)試估計該校所有學生中,閱讀時間不小于30個小時的學生人數(shù);
(III)從閱讀時間不足10個小時的樣本學生中隨機抽取3人,并用X表示其中初中生的人數(shù),求X的分布列和數(shù)學期望.
【答案】(I).a=0.03.(II).870人.
(III)所以X的分布列為:
X | 1 | 2 | 3 |
P |
|
|
|
E(X)=![]() .
.
【解析】試題分析:(1)根據(jù)各矩形面積之和為![]() ,可求得
,可求得![]() 的值;(2)先根據(jù)直方圖算出初中生中,閱讀時間不小于
的值;(2)先根據(jù)直方圖算出初中生中,閱讀時間不小于![]() 個小時的學生頻率以及高中生中,閱讀時間不小于
個小時的學生頻率以及高中生中,閱讀時間不小于![]() 個小時的學生頻率,結(jié)合總?cè)藬?shù)可估計該校所有學生中,閱讀時間不小于
個小時的學生頻率,結(jié)合總?cè)藬?shù)可估計該校所有學生中,閱讀時間不小于![]() 個小時的學生人數(shù);(3)
個小時的學生人數(shù);(3)![]() 的可能取值
的可能取值![]() ,利用組合知識結(jié)合古典概型概率公式求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得
,利用組合知識結(jié)合古典概型概率公式求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得![]() 的數(shù)學期望.
的數(shù)學期望.
試題解析:(I).a=0.03.
(II)由分層抽樣,知抽取的初中生有60名,高中生有40名.
因為初中生中,閱讀時間不小于30個小時的學生頻率為(0.02+0.005)×10=0.25,
所以所有的初中生中,閱讀時間不小于30個小時的學生約有0.25×1800=450人,
同理,高中生中,閱讀時間不小于30個小時的學生頻率為(0.03+0.005)×10=0.35,學生人數(shù)約有0.35×1200=420人.
所以該校所有學生中,閱讀時間不小于30個小時的學生人數(shù)約有450+420=870人.
(III).初中生中,閱讀時間不足10個小時的學生頻率為0.005×10=0.05,樣本人數(shù)為0.05×60=3人.
同理,高中生中,閱讀時間不足10個小時的學生樣本人數(shù)為(0.005×10)×40=2人.
故X的可能取值為l,2,3.
則P(X=1)=![]() ,P(X=2)=
,P(X=2)=![]() ,P(X=3)=
,P(X=3)=![]() .
.
所以X的分布列為:
X | 1 | 2 | 3 |
P |
|
|
|
所以E(X)=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖, ![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,
的左、右焦點, ![]() 是橢圓
是橢圓![]() 的頂點,
的頂點, ![]() 是直線
是直線![]() 與橢圓
與橢圓![]() 的另一個交點,
的另一個交點, ![]() .
.

(1)求橢圓![]() 的離心率;
的離心率;
(2)已知![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校在2010年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示。
,得到的頻率分布直方圖如圖所示。

(1)求第3、4、5組的頻率;
(2)為了能選拔出最優(yōu)秀的學生,該校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試,求第3、4、5組每組各抽取多少學生進入第二輪面試?
(3)在(2)的前提下,學校決定在這6名學生中隨機抽取2名學生接受甲考官的面試,求第4組至少有一名學生被甲考官面試的概率。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若曲線C上任意一點與直線![]() 上任意一點的距離都大于1,則稱曲線C遠離”直線
上任意一點的距離都大于1,則稱曲線C遠離”直線![]() ,在下列曲線中,“遠離”直線
,在下列曲線中,“遠離”直線![]() :y=2x的曲線有___________(寫出所有符合條件的曲線的編號)
:y=2x的曲線有___________(寫出所有符合條件的曲線的編號)
①曲線C:![]() ;②曲線C:
;②曲線C:![]() ;③曲線C:
;③曲線C:![]() ;
;
④曲線C:![]() ;⑤曲線C:
;⑤曲線C:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A、B是單位圓O上的兩點(O為圓心),∠AOB=120°,點C是線段AB上不與A、B重合的動點.MN是圓O的一條直徑,則![]() 的取值范圍是( )
的取值范圍是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四邊形ABCD是梯形,AD∥BC,∠BAD=90°,四邊形CC1D1D為矩形,已知AB⊥BC1,AD=4,AB=2,BC=1.

(I)求證:BC1∥平面ADD1;
(II)若DD1=2,求平面AC1D1與平面ADD1所成的銳二面角的余弦值;
(III)設(shè)P為線段C1D上的一個動點(端點除外),判斷直線BC1與直線CP能否垂直?并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有最大值
上有最大值![]() 和最小值
和最小值![]() .設(shè)
.設(shè)![]()
(1)求![]() 的值
的值
(2)若不等式![]() 在
在![]() 上有解,求實數(shù)
上有解,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若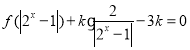 有三個不同的實數(shù)解,求實數(shù)
有三個不同的實數(shù)解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在推導很多三角恒等變換公式時,我們可以利用平面向量的有關(guān)知識來研究,在一定程度上可以簡化推理過程.如我們就可以利用平面向量來推導兩角差的余弦公式:![]()
具體過程如下:
如圖,在平面直角坐標系![]() 內(nèi)作單位圓O,以
內(nèi)作單位圓O,以![]() 為始邊作角
為始邊作角![]() .它們的終邊與單位圓O的交點分別為A,B.
.它們的終邊與單位圓O的交點分別為A,B.

則![]()
由向量數(shù)量積的坐標表示,有:
![]()
設(shè)![]() 的夾角為θ,則
的夾角為θ,則
![]()
另一方面,由圖3.1—3(1)可知,![]() ;由圖可知,
;由圖可知,

![]() .于是
.于是![]() .
.
所以![]() ,也有
,也有![]() ,
,
所以,對于任意角![]() 有:
有:![]() (
(![]() )
)
此公式給出了任意角![]() 的正弦、余弦值與其差角
的正弦、余弦值與其差角![]() 的余弦值之間的關(guān)系,稱為差角的余弦公式,簡記作
的余弦值之間的關(guān)系,稱為差角的余弦公式,簡記作![]() .
.
有了公式![]() 以后,我們只要知道
以后,我們只要知道![]() 的值,就可以求得
的值,就可以求得![]() 的值了.
的值了.
閱讀以上材料,利用下圖單位圓及相關(guān)數(shù)據(jù)(圖中M是AB的中點),采取類似方法(用其他方法解答正確同等給分)解決下列問題:
(1)判斷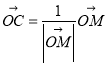 是否正確?(不需要證明)
是否正確?(不需要證明)
(2)證明:![]()
(3)利用以上結(jié)論求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com