
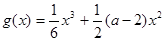 ,h(x)=2alnx,
,h(x)=2alnx,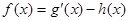 .
.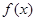 的單調性;
的單調性;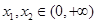 ,且
,且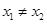 ,都有
,都有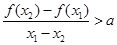
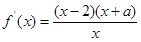
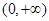 ,故只需討論分子符號,可結合二次函數的圖象判斷,此時①需討論交點
,故只需討論分子符號,可結合二次函數的圖象判斷,此時①需討論交點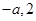 的大小,②注意根與定義域比較,所以
的大小,②注意根與定義域比較,所以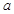 需和-2和0比較大小;(2)由對稱性,不妨設
需和-2和0比較大小;(2)由對稱性,不妨設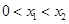 ,去分母得
,去分母得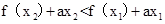 ,構造函數
,構造函數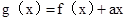 ,則其在定義域內單調遞減,故
,則其在定義域內單調遞減,故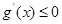 在
在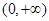 恒成立,而
恒成立,而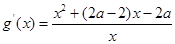 ,分子二次函數開口向上,不可能永遠小于0,故不存在.
,分子二次函數開口向上,不可能永遠小于0,故不存在.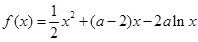 ,∴
,∴ 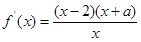 ,
, 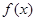 的定義域為
的定義域為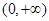 .
.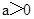 時,
時,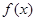 在
在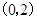 上是減函數,在在
上是減函數,在在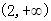 上是增函數;
上是增函數;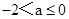 時,
時,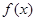 在
在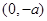 上是增函數;在
上是增函數;在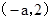 是是減函數;在
是是減函數;在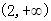 上是增函數;
上是增函數;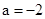 時,
時,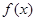 在
在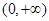 上是增函數;
上是增函數; 時,
時,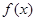 在
在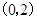 上是增函數;在
上是增函數;在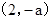 上是減函數;在
上是減函數;在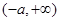 上是增函數.
上是增函數.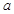 ,對任意的
,對任意的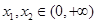 ,且
,且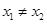 ,都有
,都有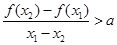 恒成立,不妨設
恒成立,不妨設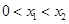 ,要使
,要使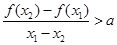 ,即
,即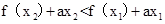 .
.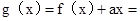
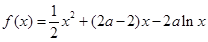 ,只要
,只要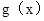 在
在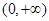 為減函數.
為減函數.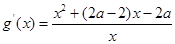 ,由題意
,由題意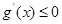 在
在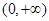 上恒成立,得
上恒成立,得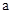 不存在.
不存在. 

 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com