
【題目】已知關(guān)于![]() 的函數(shù)
的函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)設(shè)![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若函數(shù)![]() 沒有零點(diǎn),求實(shí)數(shù)
沒有零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]()
【解析】試題分析:(1)當(dāng)![]() 時(shí),得到函數(shù)解析式
時(shí),得到函數(shù)解析式![]() ,求得
,求得![]() ,得到
,得到![]() ,得出切線的斜率,再利用點(diǎn)斜式求解直線的方程;
,得出切線的斜率,再利用點(diǎn)斜式求解直線的方程;
(2)由題意,求出![]() 的解析式,求得
的解析式,求得![]() ,可分
,可分![]() 和
和![]() 兩種情況分類討論,即可求解函數(shù)的單調(diào)區(qū)間;
兩種情況分類討論,即可求解函數(shù)的單調(diào)區(qū)間;
(3)由![]() 沒有零點(diǎn),轉(zhuǎn)化為方程
沒有零點(diǎn),轉(zhuǎn)化為方程![]() 無解,即
無解,即![]() 與
與![]() 兩圖象無交點(diǎn),列出條件,即可求解實(shí)數(shù)的取值范圍.
兩圖象無交點(diǎn),列出條件,即可求解實(shí)數(shù)的取值范圍.
試題解析:
(1)當(dāng)![]() 時(shí),
時(shí), ![]() ,
, 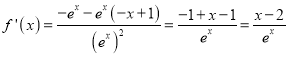 ,
,
![]() ,∴
,∴![]() ,即
,即![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .
.
(2)∵ ,
, ![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),
![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),令
時(shí),令![]() ,解得
,解得![]() ,
,
令![]() ,解得
,解得![]() ,∴
,∴![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
(3)∵![]() 沒有零點(diǎn),
沒有零點(diǎn),
即![]() 無解,∴
無解,∴![]() 與
與![]() 兩圖象無交點(diǎn),
兩圖象無交點(diǎn),
設(shè)兩圖象相切于![]() 兩點(diǎn),∴
兩點(diǎn),∴![]() ,∴
,∴![]() ,
, ![]() ,∵兩圖象無交點(diǎn),∴
,∵兩圖象無交點(diǎn),∴![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校在2016年的自主招生考試成績(jī)中隨機(jī)抽取100名學(xué)生的筆試成績(jī),被抽取學(xué)生的成績(jī)均不低于160分,且低于185分,如圖是按成績(jī)分組得到的頻率分布直方圖. 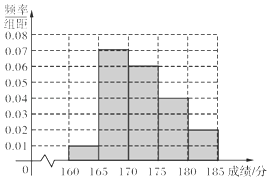
(1)為了能選拔出優(yōu)秀的學(xué)生,該校決定在筆試成績(jī)較高的第3組、第4組、第5組中用分層抽樣的方法抽取6名學(xué)生進(jìn)入第二輪面試,求第3,4,5組每組各抽取多少名學(xué)生進(jìn)入第二輪面試;
(2)在(1)的前提下,學(xué)校決定在6名學(xué)生中隨機(jī)抽取2名學(xué)生由考官A面試,求第4組至少有一名學(xué)生被考官A面試的概.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)a<1,集合A={x∈R|x>0},B={x∈R|2x2﹣3(1+a)x+6a>0},D=A∩B.
(1)求集合D(用區(qū)間表示);
(2)求函數(shù)f(x)=x2﹣(1+a)x+a在D內(nèi)的零點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)M={x| ![]() },N={x|x2+(a﹣8)x﹣8a≤0},命題p:x∈M,命題q:x∈N.
},N={x|x2+(a﹣8)x﹣8a≤0},命題p:x∈M,命題q:x∈N.
(1)當(dāng)a=﹣6時(shí),試判斷命題p是命題q的什么條件;
(2)求a的取值范圍,使命題p是命題q的一個(gè)必要但不充分條件.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】命題p:實(shí)數(shù)x滿足x2﹣4ax+3a2<0(其中a>0),命題q:實(shí)數(shù)x滿足 
(1)若a=1,且p∧q為真,求實(shí)數(shù)x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知O為坐標(biāo)原點(diǎn),設(shè)動(dòng)點(diǎn)M(2,t)(t>0).
(1)若過點(diǎn)P(0,4 ![]() )的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
)的直線l與圓C:x2+y2﹣8x=0相切,求直線l的方程;
(2)求以O(shè)M為直徑且被直線3x﹣4y﹣5=0截得的弦長(zhǎng)為2的圓的方程;
(3)設(shè)A(1,0),過點(diǎn)A作OM的垂線與以O(shè)M為直徑的圓交于點(diǎn)N,求證:線段ON的長(zhǎng)為定值,并求出這個(gè)定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某大學(xué)生在開學(xué)季準(zhǔn)備銷售一種文具盒進(jìn)行試創(chuàng)業(yè),在一個(gè)開學(xué)季內(nèi),每售出1個(gè)該產(chǎn)品獲利潤(rùn)5元,未售出的產(chǎn)品,每個(gè)虧損3元.根據(jù)歷史資料,得到開學(xué)季市場(chǎng)需求量的頻率分布直方圖如圖所示.該同學(xué)為這個(gè)開學(xué)季購(gòu)進(jìn)了160個(gè)該產(chǎn)品,以![]() (
(![]() ,單位:個(gè))表示這個(gè)開學(xué)季內(nèi)的市場(chǎng)需求量.
,單位:個(gè))表示這個(gè)開學(xué)季內(nèi)的市場(chǎng)需求量.
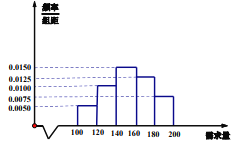
(1)根據(jù)直方圖估計(jì)這個(gè)開學(xué)季內(nèi)市場(chǎng)需求量![]() 的中位數(shù);
的中位數(shù);
(2)根據(jù)直方圖估計(jì)利潤(rùn)不少于640元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E,F(xiàn),G,H分別為AA1 , AB,BB1 , B1C1的中點(diǎn),則異面直線EF與GH所成的角等于 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,網(wǎng)格紙上小正方形的邊長(zhǎng)為1,粗線畫出的是某四面體的三視圖,則該四面體的外接球半徑為( ) 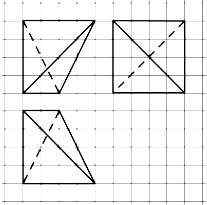
A.2 ![]()
B.![]()
C.![]()
D.2 ![]()
查看答案和解析>>