【題目】已知某快遞公司收取快遞費的標準是：重量不超過
的包裹收費
元；重量超過的包裹，在收費元的基礎上，每超過（不足，按計算）需再收
元．該快遞公司承攬了一個工藝品廠家的全部玻璃工藝品包裹的郵寄事宜，該廠家隨機統(tǒng)計了
件這種包裹的兩個統(tǒng)計數表如下：
表
包裹重量 |
|
|
|
|
|
包裹數 |
|
|
|
|
|
損壞件數 |
|
|
|
|
|
表
包裹重量 |
|
|
|
|
|
出廠價（元 |
|
|
|
|
|
賣價（元 |
|
|
|
|
|
估計該快遞公司對每件包裹收取快遞費的平均值；
將包裹重量落入各組的頻率視為概率，該工藝品廠家承擔全部運費，每個包裹只有一件產品，如果客戶收到有損壞品的包裹，該快遞公司每件按其出廠價的
賠償給廠家．現該廠準備給客戶郵寄重量在區(qū)間
和
內的工藝品各件，求該廠家這兩件工藝品獲得利潤的分布列和期望．
科目：高中數學 來源： 題型：
【題目】已知橢圓
的右焦點為F，直線l與C交于M，N兩點.
（1）若l過點F，點M，N到直線y＝2的距離分別為d1，d2，且
，求l的方程；
（2）若點M的坐標為（0，1），直線m過點M交C于另一點N′，當直線l與m的斜率之和為2時，證明：直線NN′過定點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的兩個焦點與短軸的一個端點是直角三角形的三個頂點，直線
： 
與橢圓
有且只有一個公共點．
（Ⅰ）求橢圓
的方程及點
的坐標；
（Ⅱ）設
是坐標原點，直線
平行于
，與橢圓
交于不同的兩點
、
，且與直線
交于點
，證明：存在常數
，使得
，并求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列命題：
①函數
在
上單調遞減，在
上單調遞增；
②若函數
在
上有兩個零點，則
的取值范圍是
；
③當
時，函數
的最大值為0；
④函數
在
上單調遞減；
上述命題正確的是_________（填序號）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在傳染病學中，通常把從致病刺激物侵入機體或者對機體發(fā)生作用起，到機體出現反應或開始呈現該疾病對應的相關癥狀時止的這一階段稱為潛伏期．一研究團隊統(tǒng)計了某地區(qū)1000名患者的相關信息，得到如下表格：
潛伏期（單位：天） |
|
|
|
|
|
|
|
人數 | 85 | 205 | 310 | 250 | 130 | 15 | 5 |
（1）求這1000名患者的潛伏期的樣本平均數
（同一組中的數據用該組區(qū)間的中點值作代表）；
（2）該傳染病的潛伏期受諸多因素的影響，為研究潛伏期與患者年齡的關系，以潛伏期是否超過6天為標準進行分層抽樣，從上述1000名患者中抽取200人，得到如下列聯(lián)表．請將列聯(lián)表補充完整，并根據列聯(lián)表判斷是否有
的把握認為潛伏期與患者年齡有關；
潛伏期 | 潛伏期 | 總計 | |
50歲以上（含50歲） | 100 | ||
50歲以下 | 55 | ||
總計 | 200 |
（3）以這1000名患者的潛伏期超過6天的頻率，代替該地區(qū)1名患者潛伏期超過6天發(fā)生的概率，每名患者的潛伏期是否超過6天相互獨立．為了深入硏究，該硏究團隊隨機調查了20名患者，設潛伏期超過6天的人數為
，則的期望是多少？
附：
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
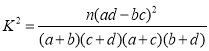，其中
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2020年寒假期間新冠肺炎肆虐，全國人民眾志成城抗擊疫情.某市要求全體市民在家隔離，同時決定全市所有學校推遲開學.某區(qū)教育局為了讓學生“停課不停學”，要求學校各科老師每天在網上授課，每天共280分鐘，請學生自主學習.區(qū)教育局為了了解高三學生網上學習情況，上課幾天后在全區(qū)高三學生中采取隨機抽樣的方法抽取了100名學生進行問卷調查，為了方便表述把學習時間在
分鐘的學生稱為
類，把學習時間在
分鐘的學生稱為
類，把學習時間在
分鐘的學生稱為
類，隨機調查的100名學生學習時間的人數頻率分布直方圖如圖所示：以頻率估計概率回答下列問題：
（1）求100名學生中，，三類學生分別有多少人？
（2）在，，三類學生中，按分層抽樣的方法從上述100個學生中抽取10人，并在這10人中任意邀請3人電話訪談，求邀請的3人中是類的學生人數的分布列和數學期望；
（3）某校高三（1）班有50名學生，某天語文和數學老師計劃分別在19:00—19:40和20:00—20:40在線上與學生交流，由于受校園網絡平臺的限制，每次只能30個人同時在線學習交流.假設這兩個時間段高三（1）班都有30名學生相互獨立地隨機登錄參加學習交流.設
表示參加語文或數學學習交流的人數，當為多少時，其概率最大.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設 
為等差數列 
的前 
項和，其中 
，且 
．
（1）求常數 
的值，并寫出 的通項公式；
（2）記 
，數列 
的前 項和為 
，若對任意的 
，都有 
，求常數 
的最小值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
