
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為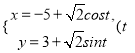 為參數),在以原點
為參數),在以原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立的極坐標系中,直線
軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求圓![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 與
與![]() 軸,
軸, ![]() 軸分別交于
軸分別交于![]() 兩點,點
兩點,點![]() 是圓
是圓![]() 上任一點,求
上任一點,求![]() 兩點的極坐標和
兩點的極坐標和![]() 面積的最小值
面積的最小值
【答案】(1)![]() ,
, ![]() ;(2)4
;(2)4
【解析】試題分析:(1)由圓C的參數方程消去t得到圓C的普通方程,由直線l的極坐標方程,利用兩角和與差的余弦函數公式化簡,根據x=ρcosθ,y=ρsinθ轉化為直角坐標方程即可;
(2)直線l與x軸,y軸的交點為A(0,2),B(﹣2,0),化為極坐標,并求出|AB|的長,根據P在圓C上,設出P坐標,利用點到直線的距離公式表示出P到直線l的距離,利用余弦函數的值域確定出最小值,即可確定出三角形PAB面積的最小值.
(1)由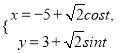 消去參數
消去參數![]() ,得
,得![]() ,
,
所以圓![]() 的普通方程為
的普通方程為![]() .
.
由![]() ,得
,得![]() ,
,
所以直線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
(2)直線![]() 與
與![]() 軸,
軸, ![]() 軸的交點為
軸的交點為![]() ,化為極坐標為
,化為極坐標為![]() ,
,
設![]() 點的坐標為
點的坐標為![]() ,則
,則![]() 點到直線
點到直線![]() 的距離為
的距離為
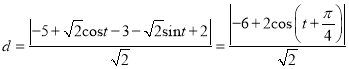 ,
,
∴![]() ,又
,又![]() ,
,
所以![]() 面積的最小值是
面積的最小值是![]() .
.


科目:高中數學 來源: 題型:
【題目】某次大型運動會的組委會為了搞好接待工作,招募了16名男志愿者和14名女志愿者,調查發現,男、女志愿者中分別有10人和6人喜愛運動,其余人不喜愛運動.
(1)根據以上數據完成下面2×2列聯表:
喜愛運動 | 不喜愛運動 | 總計 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
總計 | 30 |
(2)能否在犯錯誤的概率不超過0.10的前提下認為性別與喜愛運動有關系?
(3)已知喜歡運動的女志愿者中恰有4人會外語,如果從中抽取2人負責翻譯工作,那么抽出的志愿者中至少有1人能勝任翻譯工作的概率是多少?
參考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
參考數據:
P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益函數為R(x)= 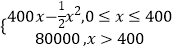 ,其中x是儀器的產量(單位:臺);
,其中x是儀器的產量(單位:臺);
(1)將利潤f(x)表示為產量x的函數(利潤=總收益﹣總成本);
(2)當產量x為多少臺時,公司所獲利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2﹣2ax+a.
(1)若對任意的實數x都有f(1+x)=f(1﹣x)成立,求實數a的值;
(2)若f(x)在區間[1,+∞)上為單調增函數,求實數a的取值范圍;
(3)當x∈[﹣1,1]時,求函數f(x)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在區間D上,如果函數f(x)為減函數,而xf(x)為增函數,則稱f(x)為D上的弱減函數.若f(x)= ![]()
(1)判斷f(x)在區間[0,+∞)上是否為弱減函數;
(2)當x∈[1,3]時,不等式 ![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若函數g(x)=f(x)+k|x|﹣1在[0,3]上有兩個不同的零點,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為得到函數y=sin(x+ ![]() )的圖象,可將函數y=sinx的圖象向左平移m個單位長度,或向右平移n個單位長度(m,n均為正數),則|m﹣n|的最小值是( )
)的圖象,可將函數y=sinx的圖象向左平移m個單位長度,或向右平移n個單位長度(m,n均為正數),則|m﹣n|的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若不等式|2x﹣1|﹣|x+a|≥a對任意的實數x恒成立,則實數a的取值范圍是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0)
,0)
D.(﹣∞,﹣ ![]() ]
]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com