
【題目】已知函數![]() ,
,![]() ,對于不相等的實數
,對于不相等的實數![]() 、
、![]() ,設
,設![]() ,
,![]() ,現有如下命題:
,現有如下命題:
①對于任意不相等的實數![]() 、
、![]() ,都有
,都有![]() ;
;
②對于任意的![]() 及任意不相等的實數
及任意不相等的實數![]() 、
、![]() ,都有
,都有![]() ;
;
③對于任意的![]() ,存在不相等的實數
,存在不相等的實數![]() 、
、![]() ,使得
,使得![]() ;
;
④對于任意的![]() ,存在不相等的實數
,存在不相等的實數![]() 、
、![]() ,使得
,使得![]() ;
;
其中所有的真命題的序號是_______.
【答案】①④
【解析】
①根據函數單調性的定義來判斷是否正確. ②通過舉反例來判斷是否正確. ③通過構造函數![]() ,利用導數研究
,利用導數研究![]() 的單調性來判斷是否正確. ④通過構造函數
的單調性來判斷是否正確. ④通過構造函數![]() ,利用導數研究
,利用導數研究![]() 的單調性來判斷是否正確.
的單調性來判斷是否正確.
對于①,由于![]() 在
在![]() 上單調遞增,根據單調性的定義可知,對于任意不相等的實數
上單調遞增,根據單調性的定義可知,對于任意不相等的實數![]() 、
、![]() ,都有
,都有![]() ,故①是真命題.
,故①是真命題.
對于②,當![]() 時,
時,![]() ,則
,則![]() ,所以②是假命題.
,所以②是假命題.
對于③,若![]() ,則
,則![]() ,即
,即![]() ,即
,即![]() ,令
,令![]() ,由于
,由于![]() ,所以
,所以![]() 不是單調函數.令
不是單調函數.令![]() ,得
,得![]() .令
.令![]() ,則由
,則由![]() 解得
解得![]() ,所以
,所以![]() 在
在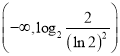 上遞減,在
上遞減,在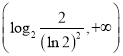 上遞增,當
上遞增,當![]() 時
時![]() 取得極小值也即是最小值,所以
取得極小值也即是最小值,所以![]() 不滿足對任意實數
不滿足對任意實數![]() 成立.所以③錯誤.
成立.所以③錯誤.
對于④,若![]() ,則
,則![]() ,即
,即![]() ,即
,即![]() ,令
,令![]() ,由于
,由于![]() ,所以
,所以![]() 不是單調函數.令
不是單調函數.令![]() ,得
,得![]() .令
.令![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 上單調遞減,值域為
上單調遞減,值域為![]() ,所以
,所以![]() 滿足對任意實數
滿足對任意實數![]() 成立.所以對于任意的
成立.所以對于任意的![]() ,存在不相等的實數
,存在不相等的實數![]() 、
、![]() ,使得
,使得![]() ,所以④為真命題.
,所以④為真命題.
故答案為:①④


科目:高中數學 來源: 題型:
【題目】![]() 年諾貝爾生理學或醫學獎獲得者威廉·凱林(WilliamG.KaelinJr)在研究腎癌的
年諾貝爾生理學或醫學獎獲得者威廉·凱林(WilliamG.KaelinJr)在研究腎癌的![]() 抑制劑過程中使用的輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下液體(滴管內液體忽略不計),設輸液開始后
抑制劑過程中使用的輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下液體(滴管內液體忽略不計),設輸液開始后![]() 分鐘,瓶內液面與進氣管的距離為
分鐘,瓶內液面與進氣管的距離為![]() 厘米,已知當
厘米,已知當![]() 時,
時,![]() .如果瓶內的藥液恰好
.如果瓶內的藥液恰好![]() 分鐘滴完.則函數
分鐘滴完.則函數![]() 的圖像為( )
的圖像為( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過點
,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點,延長
兩點,延長![]() 交橢圓
交橢圓![]() 于點
于點![]() ,
,![]() 的周長為8.
的周長為8.
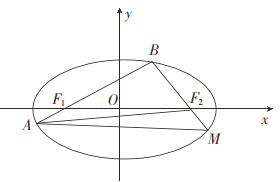
(1)求![]() 的離心率及方程;
的離心率及方程;
(2)試問:是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,四邊形![]() 是等腰梯形,
是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.將
的中點.將![]() 沿
沿![]() 折起,如圖2,點
折起,如圖2,點![]() 是棱
是棱![]() 上的點.
上的點.
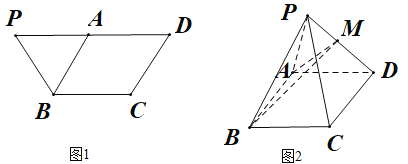
(1)若![]() 為
為![]() 的中點,證明:平面
的中點,證明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,試確定
,試確定![]() 的位置,使二面角
的位置,使二面角![]() 的余弦值等于
的余弦值等于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已定義![]() ,已知函數
,已知函數![]() 的定義域都是
的定義域都是![]() ,則下列四個命題中為真命題的是_________.(寫出所有真命題的序號)
,則下列四個命題中為真命題的是_________.(寫出所有真命題的序號)
① 若![]() 都是奇函數,則函數
都是奇函數,則函數![]() 為奇函數.
為奇函數.
② 若![]() 都是偶函數,則函數
都是偶函數,則函數![]() 為偶函數.
為偶函數.
③ 若![]() 都是增函數,則函數
都是增函數,則函數![]() 為增函數.
為增函數.
④ 若![]() 都是減函數,則函數
都是減函數,則函數![]() 為減函數.
為減函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]()
![]() 為公海與領海的分界線,一艘巡邏艇在原點
為公海與領海的分界線,一艘巡邏艇在原點![]() 處發現了北偏東
處發現了北偏東![]() 海面上
海面上![]() 處有一艘走私船,走私船正向停泊在公海上接應的走私海輪
處有一艘走私船,走私船正向停泊在公海上接應的走私海輪![]() 航行,以便上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,且兩者都是沿直線航行,但走私船可能向任一方向逃竄.
航行,以便上海輪后逃竄.已知巡邏艇的航速是走私船航速的2倍,且兩者都是沿直線航行,但走私船可能向任一方向逃竄.
(1)如果走私船和巡邏船相距6海里,求走私船能被截獲的點的軌跡;
(2)若![]() 與公海的最近距離20海里,要保證在領海內捕獲走私船,則
與公海的最近距離20海里,要保證在領海內捕獲走私船,則![]() ,
,![]() 之間的最遠距離是多少海里?
之間的最遠距離是多少海里?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)=![]() 若不建隔熱層,每年能源消耗費用為8萬元。設f(x)為隔熱層建造費用與20年的能源消耗費用之和。
若不建隔熱層,每年能源消耗費用為8萬元。設f(x)為隔熱層建造費用與20年的能源消耗費用之和。
(Ⅰ)求k的值及f(x)的表達式。
(Ⅱ)隔熱層修建多厚時,總費用f(x)達到最小,并求最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com