
設(shè)函數(shù) ,其導(dǎo)函數(shù)為
,其導(dǎo)函數(shù)為 .
.
(1)若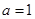 ,求函數(shù)
,求函數(shù) 在點
在點 處的切線方程;
處的切線方程;
(2)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)若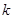 為整數(shù),若
為整數(shù),若 時,
時, 恒成立,試求
恒成立,試求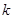 的最大值.
的最大值.
(1)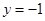 ;(2)
;(2) 的單調(diào)減區(qū)間是:
的單調(diào)減區(qū)間是: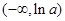 ,增區(qū)間是:
,增區(qū)間是: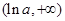 ;(3)整數(shù)k的最大值為2.
;(3)整數(shù)k的最大值為2.
解析試題分析:(1)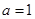 時,
時,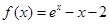 ,求導(dǎo)函數(shù)
,求導(dǎo)函數(shù)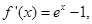 得
得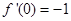 ,可得切線方程;(2)
,可得切線方程;(2)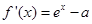 ,當
,當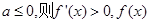 在
在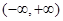 上單調(diào)遞增,當
上單調(diào)遞增,當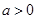 時,通過
時,通過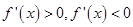 可得函數(shù)的單調(diào)區(qū)間;(3)若
可得函數(shù)的單調(diào)區(qū)間;(3)若 時,
時, 恒成立,只需
恒成立,只需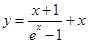 的最小值即可,
的最小值即可,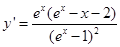 ,又
,又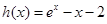 在
在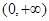 單調(diào)遞增,而
單調(diào)遞增,而 ,知
,知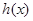 在
在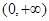 存在唯一的零點,故
存在唯一的零點,故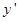 在
在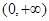 存在唯一的零點
存在唯一的零點 且
且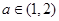 ,得
,得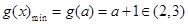 .可得整數(shù)k的最大值為2.
.可得整數(shù)k的最大值為2.
解:(1)因為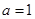 時,
時,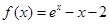 ,所以
,所以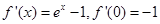 ,
,
故切線方程是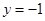
(2) 的定義域為R,
的定義域為R,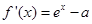 ,
,
若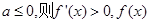 在
在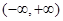 上單調(diào)遞增;
上單調(diào)遞增;
若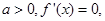 解得
解得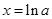 ,
,
當 變化時,
變化時,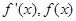 變化如下表:
變化如下表: