
【題目】在平面直角坐標系![]() 中,過定點
中,過定點![]() 作直線與拋物線
作直線與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點.
兩點.
(1)已知![]() ,若點
,若點![]() 是點
是點![]() 關于坐標原點
關于坐標原點![]() 的對稱點,求
的對稱點,求![]() 面積的最小值;
面積的最小值;
(2)是否存在垂直于![]() 軸的直線
軸的直線![]() ,使得
,使得![]() 被以
被以![]() 為直徑的圓截得的弦長恒為定值?若存在,求出
為直徑的圓截得的弦長恒為定值?若存在,求出![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
【答案】(1)![]() ;(2)滿足條件的直線
;(2)滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,詳見解析.
,詳見解析.
【解析】
(1)先得出點![]() 的坐標為
的坐標為![]() ,設
,設![]() ,
,![]() ,直線
,直線![]() 的方程為
的方程為![]() ,將直線
,將直線![]() 的方程與拋物線的方程聯立,列出韋達定理,利用三角形的面積公式求出
的方程與拋物線的方程聯立,列出韋達定理,利用三角形的面積公式求出![]() 的面積關于
的面積關于![]() 的表達式,由此可得出
的表達式,由此可得出![]() 面積的最小值;
面積的最小值;
(2)解法一:假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,求出線段
,求出線段![]() 的中點
的中點![]() 的坐標,并計算出點
的坐標,并計算出點![]() 到直線
到直線![]() 的距離以及以
的距離以及以![]() 為直徑的圓
為直徑的圓![]() 的半徑長,然后利用勾股定理可計算出
的半徑長,然后利用勾股定理可計算出![]() 截以
截以![]() 為直徑的圓所得弦長,結合弦長的表達式得出當
為直徑的圓所得弦長,結合弦長的表達式得出當![]() 時,弦長為定值,從而得出直線
時,弦長為定值,從而得出直線![]() 的方程;
的方程;
解法二:假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,求出以
,求出以![]() 為直徑的圓的方程,將直線
為直徑的圓的方程,將直線![]() 的方程與圓
的方程與圓![]() 的方程聯立,列出韋達定理,利用弦長公式計算出
的方程聯立,列出韋達定理,利用弦長公式計算出![]() 截以
截以![]() 為直徑的圓所得弦長,結合弦長的表達式得出當
為直徑的圓所得弦長,結合弦長的表達式得出當![]() 時,弦長為定值,從而得出直線
時,弦長為定值,從而得出直線![]() 的方程.
的方程.
(1)依題意,點![]() 的坐標為
的坐標為![]() ,
,
可設![]() ,
,![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
由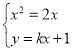 得
得![]() .
.
由韋達定理得![]() ,
,![]() .
.
于是![]() ,
,
![]() 當
當![]() 時,
時,![]() ;
;
(2)解法一:假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,
,![]() 的中點為
的中點為![]() ,
,![]() 與
與![]() 為直徑的圓相交于點
為直徑的圓相交于點![]() 、
、![]() ,
,![]() 的中點為
的中點為![]() ,則
,則![]() ,
,
![]() 點的坐標為
點的坐標為![]() ,
,![]() .
.
因為![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ,此時
,此時![]() 為定值,
為定值,
故滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,即拋物線的通徑所在的直線;
,即拋物線的通徑所在的直線;
解法2:假設滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,設以
,設以![]() 為直徑的圓上任意一點為:
為直徑的圓上任意一點為:![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
則以![]() 為直徑的圓方程為:
為直徑的圓方程為:![]() ,
,
化簡為:![]() ,
,
直線方程![]() 代入上述方程得
代入上述方程得![]()
則![]()
設直線![]() 與以
與以![]() 為直徑的圓的交點為
為直徑的圓的交點為![]() ,
,![]() ,則有
,則有
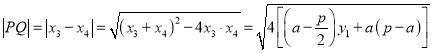
令![]() ,得
,得![]() ,此時
,此時![]() 為定值.
為定值.
故滿足條件的直線![]() 存在,其方程為
存在,其方程為![]() ,即拋物線的通徑所在的直線.
,即拋物線的通徑所在的直線.


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源: 題型:
【題目】某單位有員工1000名,平均每人每年創造利潤10萬元.為增加企業競爭力,決定優化產業結構,調整出![]() 名員工從事第三產業,調整后平均每人每年創造利潤為
名員工從事第三產業,調整后平均每人每年創造利潤為![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() .
.
(1)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(2)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤條件下,若要求調整出的員工創造出的年總利潤始終不高于剩余員工創造的年總利潤,則![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,然后縱坐標不變,橫坐標變為原來的
個單位,然后縱坐標不變,橫坐標變為原來的![]() 倍,得到
倍,得到![]() 的圖象,下面四個結論正確的是( )
的圖象,下面四個結論正確的是( )
A. 函數![]() 在區間
在區間![]() 上為增函數
上為增函數
B. 將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位后得到的圖象關于原點對稱
個單位后得到的圖象關于原點對稱
C. 點![]() 是函數
是函數![]() 圖象的一個對稱中心
圖象的一個對稱中心
D. 函數![]() 在
在![]() 上的最大值為
上的最大值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汕尾市基礎教育處為調查在校中學生每天放學后的自學時間情況,在本市的所有中學生中隨機抽取了120名學生進行調查,現將日均自學時間小于1小時的學生稱為“自學不足”者![]() 根據調查結果統計后,得到如下
根據調查結果統計后,得到如下![]() 列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為
列聯表,已知在調查對象中隨機抽取1人,為“自學不足”的概率為![]() .
.
非自學不足 | 自學不足 | 合計 | |
配有智能手機 | 30 | ||
沒有智能手機 | 10 | ||
合計 |
![]() 請完成上面的列聯表;
請完成上面的列聯表;
![]() 根據列聯表的數據,能否有
根據列聯表的數據,能否有![]() 的把握認為“自學不足”與“配有智能手機”有關?
的把握認為“自學不足”與“配有智能手機”有關?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線l的參數方程為
中,直線l的參數方程為![]() (t為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程
(t為參數).以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程![]() .
.
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)若直線l與曲線C交于A,B兩點,![]() 為直線l上一點,求
為直線l上一點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線方程為y2=-4x,直線l的方程為2x+y-4=0,在拋物線上有一動點A,點A到y軸的距離為m,到直線l的距離為n,則m+n的最小值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】啟東市政府擬在蝶湖建一個旅游觀光項目,設計方案如下:如圖所示的圓O是圓形湖的邊界,沿線段AB,BC,CD,DA建一個觀景長廊,其中A,B,C,D是觀景長廊的四個出入口且都在圓O上,已知:BC=12百米,AB=8百米,在湖中P處和湖邊D處各建一個觀景亭,且它們關于直線AC對稱,在湖面建一條觀景橋APC.觀景亭的大小、觀景長廊、觀景橋的寬度均忽略不計,設![]() .
.
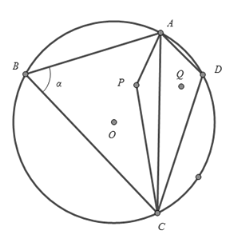
(1)若觀景長廊AD=4百米,CD=AB,求由觀景長廊所圍成的四邊形ABCD內的湖面面積;
(2)當![]() 時,求三角形區域ADC內的湖面面積的最大值;
時,求三角形區域ADC內的湖面面積的最大值;
(3)若CD=8百米且規劃建亭點P在三角形ABC區域內(不包括邊界),試判斷四邊形ABCP內湖面面積是否有最大值?若有,求出最大值,并寫出此時![]() 的值;若沒有,請說明理由.
的值;若沒有,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓C:
中,橢圓C:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,P為橢圓C上一點,且
,P為橢圓C上一點,且![]() 垂直于
垂直于![]() 軸,連結
軸,連結![]() 并延長交橢圓于另一點
并延長交橢圓于另一點![]() ,設
,設![]()
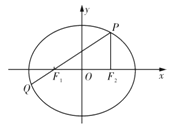
(1)若點![]() 的坐標為
的坐標為![]() ,求橢圓
,求橢圓![]() 的方程;
的方程;
(2)若![]() ,求橢圓
,求橢圓![]() 的離心率的取值范圍
的離心率的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
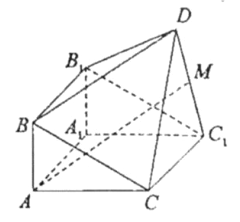
【題目】如圖,由直三棱柱![]() 和四棱錐
和四棱錐![]() 構成的幾何體中,
構成的幾何體中,![]() ,平面
,平面![]() 平面
平面![]()
(I)求證:![]() ;
;
(II)若M為![]() 中點,求證:
中點,求證:![]() 平面
平面![]() ;
;
(III)在線段BC上(含端點)是否存在點P,使直線DP與平面![]() 所成的角為
所成的角為![]() ?若存在,求
?若存在,求![]() 得值,若不存在,說明理由.
得值,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com