Question

【題目】甲乙兩位同學整理了某學科高三以來9次考試的成績（甲缺席了其中3次考試，只有6次成績），得到如下莖葉圖.

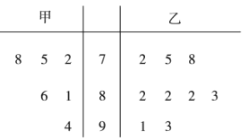
（1）若用分層抽樣的方法從兩人的15個成績選取5個評估，應選取甲的幾次成績？若分層抽樣時對甲的成績采用隨機抽取，求選取到的甲的成績至少有一次高于85分的概率；

（2）試通過表中的所有數據，從平均水平和穩定性來評判兩位同學該學科的考試成績.

Answer 1

【答案】（1）（2）乙的平均分比甲更高，穩定性也更好，綜合認為，乙的更好。

【解析】

（1）按照比例，應該取甲的2次成績．設甲的6個成績由高到低為A，B，C，D，E，F，高于85分的是A，B兩個，利用列舉法能求出選取到的甲的成績至少有一次高于85分的概率．

（2）先計算出甲的均值為81分，乙的均值為82分，由此求出甲的方差和乙的方差，從而得到乙的平均分比甲更高，穩定性也更好，綜合認為乙的更好．

（1）因為甲乙考試次數比例為，所以抽取5個成績，應該取甲的2次成績；

設甲的6個成績由高到低為，，，，，，高于85分的是，兩個，

則取法有，，，，，，，，，，，，，，共15種，

其中至少有一次高于85分的有，，，，，，，，共9種，概率為.

（2）甲的均值為分，

乙的均值為分，

所以甲的方差為，

乙的方差為，

所以乙的平均分比甲更高，穩定性也更好，綜合認為，乙的更好.