Question

若方程x²＋(m－2)x－m＋5＝0的兩個根都大于2，求實數m的取值范圍．

閱讀下面的解法，回答提出的問題．

解：第一步，令判別式Δ＝(m－2)²－4(－m＋5)≥0，

解得m≥4或m≤－4；

第二步，設兩根為x₁，x₂，由x₁＞2，x₂＞2得

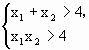，所以．

所以m＜－2．

第三步，由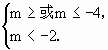得m≤－4．

第四步，由第三步得出結論．

當m∈(－∞，－4]時，此方程兩根均大于2．

但當取m＝－6檢驗知，方程x²－8x＋11＝0兩根為x＝4±，其中4－＜2．

試問：產生錯誤的原因是什么？

Answer 1

答案：
解析：

m的取值范圍為－5＜m≤－4．