
【題目】2020年,我國繼續實行個人所得稅專項附加扣除辦法,涉及子女教育、繼續教育、大病醫療、住房貸款利息、住房租金、贍養老人等六項專項附加扣除.某單位老、中、青員工分別有![]() 人,現采用分層抽樣的方法,從該單位上述員工中抽取50人調查專項附加扣除的享受情況.
人,現采用分層抽樣的方法,從該單位上述員工中抽取50人調查專項附加扣除的享受情況.
(Ⅰ)應從老、中、青員工中分別抽取多少人?
(Ⅱ)抽取的50人中,享受至少兩項專項附加扣除的員工有5人,分別記為![]() .享受情況如下表,其中“○”表示享受,“×”表示不享受.現從這5人中隨機抽取2人接受采訪.
.享受情況如下表,其中“○”表示享受,“×”表示不享受.現從這5人中隨機抽取2人接受采訪.
員工 項目 | A | B | C | D | E |
子女教育 | ○ | ○ | × | ○ | × |
繼續教育 | × | × | ○ | × | ○ |
大病醫療 | × | ○ | × | ○ | × |
住房貸款利息 | ○ | ○ | × | × | ○ |
住房租金 | × | × | ○ | ○ | × |
贍養老人 | ○ | ○ | × | × | × |
(1)試用所給字母列舉出所有可能的抽取結果;
(2)設![]() 為事件“抽取的2人享受的專項附加扣除全都不相同”,求事件
為事件“抽取的2人享受的專項附加扣除全都不相同”,求事件![]() 發生的概率.
發生的概率.
【答案】(Ⅰ)12人、18人和20人;(Ⅱ)(1)所有可能的抽取結果有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10種;(2)![]() .
.
【解析】
(Ⅰ)根據分層抽樣的方法,即可求解老、中、青員工中分別抽取的人數;
(Ⅱ)(1)從已知的5人中隨機抽取2人,利用列舉法,即可求得所有的基本事件;
(2)由表格中數據,利用列舉法得到符合題意的所有基本事件,利用古典概型的概率計算公式,即可求解.
(Ⅰ)由題意,單位老、中、青員工共有![]() 人,
人,
根據分層抽樣的分法,可得:老年員工應抽取人![]() 人,
人,
中年員工應抽取![]() 人,青年員工應抽取
人,青年員工應抽取![]() 人
人
(Ⅱ)(1) 從編號為![]() 的5人中隨機抽取2人接受采訪,可得所有可能的抽取結果有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共有10種.
的5人中隨機抽取2人接受采訪,可得所有可能的抽取結果有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共有10種.
(2)由題中表格可知,事件M包含的基本事件只有AC,BC,DE,共有3種,
所以事件![]() 發生的概率
發生的概率![]() .
.


科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,側面
中,側面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據權威部門統計,高中學生眼睛近視已是普遍現象,這與每個學生是否科學用眼有很大關系.每年5月5日是全國愛眼日,我市某中學在此期間開展了一系列的用眼衛生教育活動.為了解本校學生用眼衛生情況,學校醫務室隨機抽取了100名學生對其進行調查,下面是根據調查結果繪制的學生不間斷用眼時間(單位:分鐘)的頻率分布直方圖,且將不間斷用眼時間不低于60分鐘的學生稱為“不愛護眼者”,低于60分鐘的學生稱為“愛護眼者”.
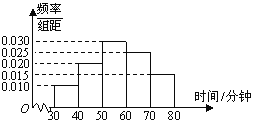
(1)根據頻率分布直方圖,求這100名學生不間斷用眼時間的平均數和中位數(結果精確到0.1);
(2)根據已知條件完成下面2×2列聯表,并據此判斷是否有99%的把握認為“不愛護眼者”與性別有關?
愛護眼者 | 不愛護眼者 | 合計 | |
男 | 45 | ||
女 | 15 | ||
合計 |
(3)在不間斷用眼時間為![]() 和
和![]() 兩組人中先按分層抽樣的方法任意選取5人,再從這5人中隨機抽取2人了解他們的視力狀況,求這兩人來自不同組別的概率.
兩組人中先按分層抽樣的方法任意選取5人,再從這5人中隨機抽取2人了解他們的視力狀況,求這兩人來自不同組別的概率.
附:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 的左右焦點,點
的左右焦點,點![]() 在橢圓上,且
在橢圓上,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 分別交橢圓
分別交橢圓![]() 于
于![]() 和
和![]() ,且
,且![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 等差數列?若存在,求出的值,若不存在,請說明理由.
等差數列?若存在,求出的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,某地出土的一種“釘”是由四條線段組成,其結構能使它任意拋至水平面后,總有一端所在的直線豎直向上,并記組成該“釘”的四條線段的公共點為O,釘尖為![]() .
.
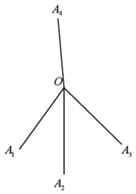
⑴設![]() ,當
,當![]() ,
,![]() ,
,![]() 在同一水平面內時,求
在同一水平面內時,求![]() 與平面
與平面![]() 所成角的大小
所成角的大小![]() 結果用反三角函數值表示
結果用反三角函數值表示![]() .
.
⑵若該“釘”的三個釘尖所確定的三角形的面積為![]() ,要用某種線型材料復制100枚這種“釘”
,要用某種線型材料復制100枚這種“釘”![]() 損耗忽略不計
損耗忽略不計![]() ,共需要該種材料多少米?
,共需要該種材料多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市在節日期間進行有獎促銷,規定凡在該超市購物滿400元的顧客,均可獲得一次摸獎機會.摸獎規則如下:獎盒中放有除顏色不同外其余完全相同的4個球(紅、黃、黑、白).顧客不放回的每次摸出1個球,若摸到黑球則摸獎停止,否則就繼續摸球.按規定摸到紅球獎勵20元,摸到白球或黃球獎勵10元,摸到黑球不獎勵.
(1)求1名顧客摸球2次摸獎停止的概率;
(2)記X為1名顧客摸獎獲得的獎金數額,求隨機變量X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com