
【題目】如圖1~4,在直角邊分別為3和4的直角三角形中,每多作一條斜邊上的高就增加一個三角形的內切圓,依此類推,圖10中有10個直角三角形的內切圓,它們的面積分別記為S1 , S2 , S3 , …,S10 , 則S1+S2+S3+…+S10=
【答案】π
【解析】解:(1)圖1,
過點O做OE⊥AC,OF⊥BC,垂足為E、F,則∠OEC=∠OFC=90°
∵∠C=90°
∴四邊形OECF為矩形
∵OE=OF
∴矩形OECF為正方形
設圓O的半徑為r,則OE=OF=r,AD=AE=3﹣r,BD=4﹣r
∴3﹣r+4+r=5,r= ![]() =1
=1
∴S1=π×12=π
2)圖2,
由S△ABC= ![]() ×3×4=
×3×4= ![]() ×5×CD
×5×CD
∴CD= ![]()
由勾股定理得:AD= ![]() =
= ![]() ,BD=5﹣
,BD=5﹣ ![]() =
= ![]()
由(1)得:⊙O的半徑= ![]() =
= ![]() ,⊙E的半徑=
,⊙E的半徑= ![]() =
= ![]()
∴S1+S2=π× ![]() +π×
+π× ![]() =π
=π
3)圖3,
由S△CDB= ![]() ×
× ![]() ×
× ![]() =
= ![]() ×4×MD
×4×MD
∴MD= ![]()
由勾股定理得:CM= ![]() =
= ![]() ,MB=4﹣
,MB=4﹣ ![]() =
= ![]()
由(1)得:⊙O的半徑= ![]() ,:⊙E的半徑=
,:⊙E的半徑= ![]() =
= ![]() ,:⊙F的半徑=
,:⊙F的半徑= ![]() =
= ![]()
∴S1+S2+S3=π× ![]() +π×
+π× ![]() +π×
+π× ![]() =π
=π
∴圖4中的S1+S2+S3+S4=π
則S1+S2+S3+…+S10=π
故答案為:π.
(1)圖1,作輔助線構建正方形OECF,設圓O的半徑為r,根據切線長定理表示出AD和BD的長,利用AD+BD=5列方程求出半徑r= ![]() (a、b是直角邊,c為斜邊),運用圓面積公式=πr2求出面積=π;(2)圖2,先求斜邊上的高CD的長,再由勾股定理求出AD和BD,利用半徑r=
(a、b是直角邊,c為斜邊),運用圓面積公式=πr2求出面積=π;(2)圖2,先求斜邊上的高CD的長,再由勾股定理求出AD和BD,利用半徑r= ![]() (a、b是直角邊,c為斜邊)求兩個圓的半徑,從而求出兩圓的面積和=π;(3)圖3,繼續求高DM和CM、BM,利用半徑r=
(a、b是直角邊,c為斜邊)求兩個圓的半徑,從而求出兩圓的面積和=π;(3)圖3,繼續求高DM和CM、BM,利用半徑r= ![]() (a、b是直角邊,c為斜邊)求三個圓的半徑,從而求出三個圓的面積和=π;綜上所述:發現S1+S2+S3+…+S10=π.
(a、b是直角邊,c為斜邊)求三個圓的半徑,從而求出三個圓的面積和=π;綜上所述:發現S1+S2+S3+…+S10=π.


科目:高中數學 來源: 題型:
【題目】根據環境保護部《環境空氣質量指數(![]() )技術規定》,空氣質量指數(
)技術規定》,空氣質量指數(![]() )在201—300之間為重度污染;在301—500之間為嚴重污染.依據空氣質量預報,同時綜合考慮空氣污染程度和持續時間,將空氣重污染分4個預警級別,由輕到重依次為預警四級、預警三級、預警二級、預警一級,分別用藍、黃、橙、紅顏色標示,預警一級(紅色)為最高級別.(一)預警四級(藍色):預測未來1天出現重度污染;(二)預警三級(黃色):預測未來1天出現嚴重污染或持續3天出現重度污染;(三)預警二級(橙色);預測未來持續3天交替出現重度污染或嚴重污染;(四)預警一級(紅色);預測未來持續3天出現嚴重污染.
)在201—300之間為重度污染;在301—500之間為嚴重污染.依據空氣質量預報,同時綜合考慮空氣污染程度和持續時間,將空氣重污染分4個預警級別,由輕到重依次為預警四級、預警三級、預警二級、預警一級,分別用藍、黃、橙、紅顏色標示,預警一級(紅色)為最高級別.(一)預警四級(藍色):預測未來1天出現重度污染;(二)預警三級(黃色):預測未來1天出現嚴重污染或持續3天出現重度污染;(三)預警二級(橙色);預測未來持續3天交替出現重度污染或嚴重污染;(四)預警一級(紅色);預測未來持續3天出現嚴重污染.
某城市空氣質量監測部門對近300天空氣中![]() 濃度進行統計,得出這300天
濃度進行統計,得出這300天![]() 濃度的頻率分布直方圖如圖,將
濃度的頻率分布直方圖如圖,將![]() 濃度落入各組的頻率視為概率,并假設每天的
濃度落入各組的頻率視為概率,并假設每天的![]() 濃度相互獨立.
濃度相互獨立.
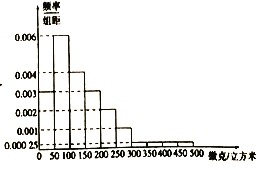
(1)求當地監測部門發布顏色預警的概率;
(2)據當地監測站數據顯示未來4天將出現3天嚴重污染,求監測部門發布紅色預警的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,側面
的正方形,側面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.

(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:面![]() 平面
平面![]() ;
;
(3)在線段![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某知名連鎖店分店開張營業期間,在固定的時間段內消費達到一定標準的顧客可進行一次抽獎活動,隨著抽獎活動的有效展開,參與抽獎活動的人數越來越多,該分店經理對開業前7天參加抽獎活動的人數進行統計,![]() 表示開業第
表示開業第![]() 天參加抽獎活動的人數,得到統計表格如下:
天參加抽獎活動的人數,得到統計表格如下:

經過進一步的統計分析,發現![]() 與
與![]() 具有線性相關關系.
具有線性相關關系.
(1)根據上表給出的數據,用最小二乘法,求出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若該分店此次抽獎活動自開業始,持續10天,參加抽獎的每位顧客抽到一等獎(價值200元獎品)的概率為![]() ,抽到二等獎(價值100元獎品)的概率為
,抽到二等獎(價值100元獎品)的概率為![]() ,抽到三等獎(價值10元獎品)的概率為
,抽到三等獎(價值10元獎品)的概率為![]() ,試估計該分店在此次抽獎活動結束時送出多少元獎品?
,試估計該分店在此次抽獎活動結束時送出多少元獎品?
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某校高一年級學生參加社區服務次數進行統計,隨機抽取![]() 名學生作為樣本,得到這
名學生作為樣本,得到這![]() 名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
名學生參加社區服務的次數.根據此數據作出了頻數與頻率的統計表和頻率分布直方圖如下:
分組 | 頻數 | 頻率 |
| 10 | 0.25 |
| 25 |
|
|
|
|
| 2 | 0.05 |
合計 |
| 1 |

(1)求出表中![]() 及圖中
及圖中![]() 的值;
的值;
(2)試估計他們參加社區服務的平均次數;
(3)在所取樣本中,從參加社區服務的次數不少于20次的學生中任選2人,求至少1人參加社區服務次數在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三文科500名學生參加了5月份的模擬考試,學校為了了解高三文科學生的數學、語文情況,利用隨機數表法從中抽取100名學生的成績進行統計分析,抽出的100名學生的數學、語文成績如下表:

(1)將學生編號為:001,002,003,……,499,500.若從第5行第5列的數開始右讀,請你依次寫出最先抽出的5個人的編號(下面是摘自隨機數表的第4行至第7行)

(2)若數學的優秀率為![]() ,求
,求![]() 的值;
的值;
(3)在語文成績為良好的學生中,已知![]() ,求數學成績“優”比“良”的人數少的概率.
,求數學成績“優”比“良”的人數少的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com