【題目】四名同學根據各自的樣本數據研究變量
之間的相關關系，并求得回歸直線方程，分別得到以下四個結論：( )
①
與
負相關且
. ②
與
負相關且
③
與
正相關且
④
與
正相關且
其中正確的結論的序號是（ ）
A. ①② B. ②③ C. ①④ D. ③④
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=1﹣ 
（a＞0且a≠1）是定義在R上的奇函數．
（1）求a的值；
（2）求f（x）的值域；
（3）若關于x的方程|f（x）（2x+1）|=m有1個實根，求實數m的取值范圍；
（4）當x∈（0，1]時，tf（x）≥2x﹣2恒成立，求實數t取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】血藥濃度（Plasma Concentration）是指藥物吸收后在血漿內的總濃度. 藥物在人體內發揮治療作用時，該藥物的血藥濃度應介于最低有效濃度和最低中毒濃度之間.已知成人單次服用1單位某藥物后，體內血藥濃度及相關信息如圖所示：
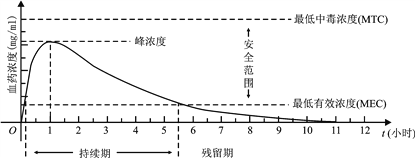
根據圖中提供的信息，下列關于成人使用該藥物的說法中，不正確的是
A. 首次服用該藥物1單位約10分鐘后，藥物發揮治療作用
B. 每次服用該藥物1單位，兩次服藥間隔小于2小時，一定會產生藥物中毒
C. 每間隔5.5小時服用該藥物1單位，可使藥物持續發揮治療作用
D. 首次服用該藥物1單位3小時后，再次服用該藥物1單位，不會發生藥物中毒
查看答案和解析>>
科目：高中數學 來源： 題型：
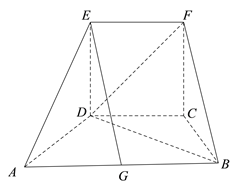
【題目】如圖所示的幾何體中，四邊形
為等腰梯形， 
∥
， 
， 
，四邊形
為正方形，平面
平面
.
（Ⅰ）若點
是棱
的中點，求證： 
∥平面
；
（Ⅱ）求直線
與平面
所成角的正弦值；
（Ⅲ）在線段
上是否存在點
，使平面
平面
？若存在，求
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在國家“大眾創業，萬眾創新”戰略下，某企業決定加大對某種產品的研發投入，已知研發投入
(十萬元)與利潤
(百萬元)之間有如下對應數據：
| 2 | 3 | 4 | 5 | 6 |
| 2 | 4 | 5 | 6 | 7 |
若由資料知
對
呈線性相關關系。試求：
（1）線性回歸方程
；
（2）估計
時，利潤是多少？
附：利用“最小二乘法”計算a,b的值時,可根據以下公式：
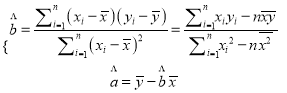
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
．
（1）判斷函數f（x）在區間[1，+∞）上的單調性，并用定義證明你的結論；
（2）求函數f（x）在區間[2，4]上的最大值與最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
