
方程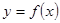 的曲線如圖所示,那么方程
的曲線如圖所示,那么方程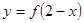 的曲線是( )
的曲線是( )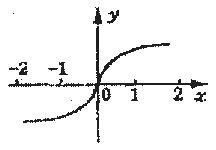
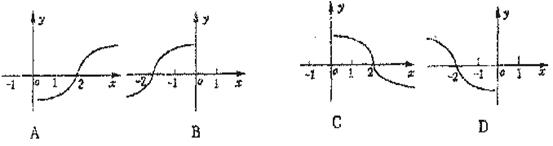
C
解析試題分析:跟據方程f(x,y)=0的曲線和方程f(2-x,y)=0的曲線中x系數互為相反數,作出函數f(x,y)=0關于y軸對稱的函數的圖象,曲線f(-x,y)和函數y=f(2-x,y)中x的系數不是1,故把-1提出,看x的變化,決定了左右平移的方向和平移的長度.
解:先作出f(x,y)=0關于y軸對稱的函數的圖象,
即為函數f(-x,y)=0的圖象,
又f(2-x,y)=0即為f(-(x-2),y)=0,
即由f(-x,y)=0向右平移2個單位,故選C.
考點:函數圖像的變換
點評:考查函數圖象的平移變換對稱變換和識圖能力,注意左右平移時,不僅要注意作加右減,更要注意x的系數是否為1,不是1的時候,一定先提出系數,再平移,體現了數形結合和運動變化的思想,屬基礎題易錯題.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案科目:高中數學 來源: 題型:單選題
如果若干個函數的圖象經過平移后能夠重合,則稱這些函數為“互為生成函數”。給出下列函數①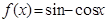 ;②
;②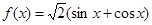 ;③
;③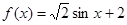 ;④
;④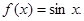 其中“互為生成函數”的是( )
其中“互為生成函數”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com