【題目】已知函數
.
（1）已知直線
：
，
：
若直線
與關于對稱，又函數
在
處的切線與平行，求實數
的值；
（2）若
，證明：當
時，
恒成立.
【答案】（1）
；（2）見解析.
【解析】
（1）首先利用直線
一定過
與
的交點，再利用直線上任意點關于對稱的點都在直線上，之后應用兩點是式求得直線的方程，求得其斜率，即為函數
的值，從而求得結果；
（2）利用導數研究函數的單調性，從而證得結果.
（1）由
解得
必過與的交點
.
在上取點
，易得點關于對稱的點為
，
即為直線
，所以的方程為
，
即
，其斜率為
.
又
，
所以函數
在
處的切線的斜率為
，
由題意可得
，解得
.
（2）法一：因為
所以，
①若
，
.∴在
上單調遞減.
②若
，當
，
或
時，
時，
當
時，
.
∴在
，
上單調遞減，在
上單調遞增.
綜上，當
時，函數在上單調遞減，
所以
，又
所以，當時，
恒成立.
法二：要證，即證
，
因為
，即證
.
∵，∴
.
設
，則
.
設
，則
，
在上，
恒成立.
∴
在上單調遞增.
又∵
，∴
時，
，
所以
在上單調遞增，
∴
，∴
，
，
所以
，
所以在上恒成立.
即當時，恒成立.
綜上，當時，恒成立.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，己知圓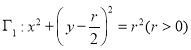
和雙曲線
，記
與
軸正半軸、
軸負半軸的公共點分別為
、
，又記與
在第一、第四象限的公共點分別為
、
.
（1）若
，且恰為的左焦點，求的兩條漸近線的方程；
（2）若，且
，求實數
的值；
（3）若恰為的左焦點，求證：在軸上不存在這樣的點
，使得
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
的右頂點為A，上頂點為B．已知橢圓的離心率為
，
．
（1）求橢圓的方程；
（2）設直線
與橢圓交于
，
兩點，
與直線
交于點M，且點P，M均在第四象限．若
的面積是
面積的2倍，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
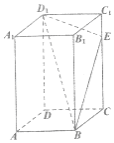
【題目】如圖，已知在長方體
中，
，
，
，點
為
上的一個動點，平面
與棱
交于點
，給出下列命題：
①四棱錐
的體積為20；
②存在唯一的點，使截面四邊形
的周長取得最小值
；
③當點不與
，
重合時，在棱
上均存在點
，使得
平面；
④存在唯一的點，使得
平面，且
．
其中正確的命題是_____（填寫所有正確的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
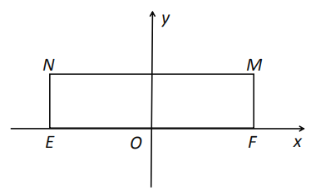
【題目】已知矩形EFMN，
，
，以EF的中點O為原點，建立如圖的平面直角坐標系，若橢圓
以E，F為焦點，且經過M，N兩點.
（1）求橢圓的方程；
（2）直線
與相交于A，B兩點，在y軸上是否存在點C，使得△ABC為正三角形，若存在，求出l的方程；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過曲線C1：
(a＞0，b＞0)的左焦點F1作曲線C2：x2＋y2＝a2的切線，設切點為M，直線F1M交曲線C3：y2＝2px(p＞0)于點N，其中曲線C1與C3有一個共同的焦點，若|MF1|＝|MN|，則曲線C1的離心率為( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著經濟的發展，城市空氣質量也越來越引起了人民的關注，如圖是我國某大城市2018年1月至8月份的空氣質量檢測結果，圖中一、二、三、四級是空氣質量等級，一級空氣質量最好，一級和二級都是空氣質量合格，下面說法錯誤的是（ ）
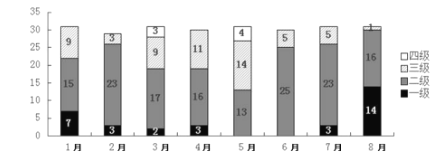
A.6月的空氣質量最差
B.8月是空氣質量最好的一個月
C.第二季度與第一季度相比，空氣質量合格天數的比重下降了
D.1月至8月空氣質量合格天數超過20天的月份有5個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐V﹣ABCD中，底面ABCD是菱形，對角線AC與BD交于點O，VO⊥平面ABCD，E是棱VC的中點．
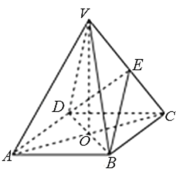
（1）求證：VA∥平面BDE；
（2）求證：平面VAC⊥平面BDE．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
