
某分公司經銷某種品牌產品,每件產品的成本為30元,并且每件產品須向總公司繳納a元(a為常數,2≤a≤5)的管理費,根據多年的統計經驗,預計當每件產品的售價為x元時,產品一年的銷售量為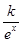 (e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(e為自然對數的底數)萬件,已知每件產品的售價為40元時,該產品一年的銷售量為500萬件.經物價部門核定每件產品的售價x最低不低于35元,最高不超過41元.
(Ⅰ)求分公司經營該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;
(Ⅱ)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,并求出L(x)的最大值.
參考公式: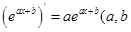 為常數
為常數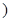 .
.
(Ⅰ)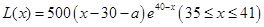 ;(Ⅱ)每件產品的售價為(31+a)元時,該產品一年的利潤最大,最大利潤為
;(Ⅱ)每件產品的售價為(31+a)元時,該產品一年的利潤最大,最大利潤為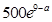 萬元.
萬元.
解析試題分析:(Ⅰ)求分公司經營該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式,由該產品一年的銷售量為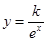 ,將每件產品的售價為40元時,該產品一年的銷售量為500萬件,代入可得k值,進而根據利潤=單件利潤×銷售量得到該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;(Ⅱ)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,由(Ⅰ)中所得函數的解析式,求導后分析函數的單調性,進而分析出該產品一年的利潤L(x)的最大值.
,將每件產品的售價為40元時,該產品一年的銷售量為500萬件,代入可得k值,進而根據利潤=單件利潤×銷售量得到該產品一年的利潤L(x)萬元與每件產品的售價x元的函數關系式;(Ⅱ)當每件產品的售價為多少元時,該產品一年的利潤L(x)最大,由(Ⅰ)中所得函數的解析式,求導后分析函數的單調性,進而分析出該產品一年的利潤L(x)的最大值.
試題解析:(Ⅰ)由題意,該產品一年的銷售量為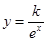 ,將
,將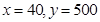 代入得
代入得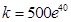 ,故該產品一年的銷售量為
,故該產品一年的銷售量為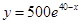 2分
2分
故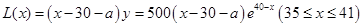 , 6分
, 6分
(Ⅱ)由(Ⅰ)得,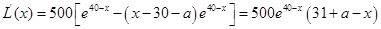 ,
,
當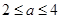 時,
時,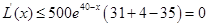 ,當且僅當
,當且僅當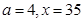 時取等號,故
時取等號,故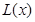 在
在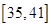 上單調遞減,故
上單調遞減,故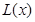 的最大值為
的最大值為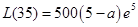 9分
9分
當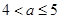 時,
時,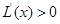 ?
?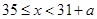 ,
,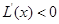 ?
?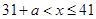 ,故
,故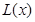 在
在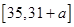 上單調遞增,在
上單調遞增,在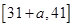 上單調遞減,故
上單調遞減,故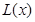 的最大值為
的最大值為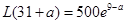 a12分綜上所述,當
a12分綜上所述,當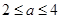 時,每件產品的售價為35元時,該產品一年的利潤最大,最大利潤為
時,每件產品的售價為35元時,該產品一年的利潤最大,最大利潤為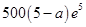 萬元;當
萬元;當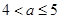 時,每件產品的售價為(31+a)元時,該產品一年的利潤最大,最大利潤為
時,每件產品的售價為(31+a)元時,該產品一年的利潤最大,最大利潤為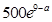 萬元; 14分
萬元; 14分
考點:函數模型的選擇與應用.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:解答題
對于函數 若存在
若存在 ,使得
,使得 成立,則稱
成立,則稱 為
為 的不動點.
的不動點.
已知
(1)當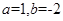 時,求函數
時,求函數 的不動點;
的不動點;
(2)若對任意實數 ,函數
,函數 恒有兩個相異的不動點,求
恒有兩個相異的不動點,求 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若 圖象上
圖象上 、
、 兩點的橫坐標是函數
兩點的橫坐標是函數 的不動點,且
的不動點,且 、
、 兩點關于直線
兩點關于直線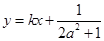 對稱,求
對稱,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“城中觀海”是近年來國內很多大中型城市內澇所致的現象,究其原因,除天氣因素、城市規劃等原因外,城市垃圾雜物也是造成內澇的一個重要原因。暴雨會沖刷城市的垃圾雜物一起進入下水道,據統計,在不考慮其它因素的條件下,某段下水道的排水量V(單位:立方米/小時)是雜物垃圾密度x(單位:千克/立方米)的函數。當下水道的垃圾雜物密度達到2千克/立方米時,會造成堵塞,此時排水量為0;當垃圾雜物密度不超過0.2千克/立方米時,排水量是90立方米/小時;研究表明,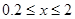 時,排水量V是垃圾雜物密度x的一次函數。
時,排水量V是垃圾雜物密度x的一次函數。
(Ⅰ)當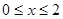 時,求函數V(x)的表達式;
時,求函數V(x)的表達式;
(Ⅱ)當垃圾雜物密度x為多大時,垃圾雜物量(單位時間內通過某段下水道的垃圾雜物量,單位:千克/小時) 可以達到最大,求出這個最大值。
可以達到最大,求出這個最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數 滿足對任意實數
滿足對任意實數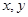 都有
都有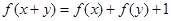 成立,且當
成立,且當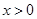 時,
時,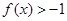 ,
,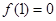 .
.
(1)求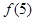 的值;
的值;
(2)判斷 在
在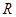 上的單調性,并證明;
上的單調性,并證明;
(3)若對于任意給定的正實數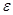 ,總能找到一個正實數
,總能找到一個正實數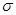 ,使得當
,使得當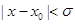 時,
時,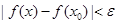 ,則稱函數
,則稱函數 在
在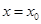 處連續。試證明:
處連續。試證明: 在
在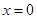 處連續.
處連續.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com