【題目】《九章算術·均輸》中有如下問題：“今有五人分十錢，令上二人所得與下三人等，問各得幾何．”其意思為“已知甲、乙、丙、丁、戊五人分10錢，甲、乙兩人所得與丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差數(shù)列，問五人各得多少錢？”（“錢”是古代的一種重量單位）．這個問題中，甲所得為（ ）
A.
錢B.
錢C.
錢D.
錢
科目：高中數(shù)學 來源： 題型：
【題目】如圖，正方體ABCD﹣A1B1C1D1的棱長為1，線段B1D1上有兩個動點E、F，且EF=
．則下列結論中正確的個數(shù)為
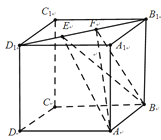
①AC⊥BE；
②EF∥平面ABCD；
③三棱錐A﹣BEF的體積為定值；
④
的面積與
的面積相等，
A.4B.3C.2D.1
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的準線與x軸的交點為H，點F為拋物線的焦點，點P在拋物線上且
，當k最大時，點P恰好在以H，F為焦點的雙曲線上，則k的最大值為_____，此時該雙曲線的離心率為_____．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的準線與x軸的交點為H，點F為拋物線的焦點，點P在拋物線上且
，當k最大時，點P恰好在以H，F為焦點的雙曲線上，則k的最大值為_____，此時該雙曲線的離心率為_____．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，其中a為非零常數(shù)．
討論
的極值點個數(shù)，并說明理由；
若
，
證明：在區(qū)間
內有且僅有1個零點；
設
為的極值點，
為的零點且
，求證：
．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左頂點為
，右焦點為
，點
在橢圓
上．
（1）求橢圓的方程；
（2）若直線
與橢圓交于
兩點，直線
分別與
軸交于點
，在
軸上，是否存在點
，使得無論非零實數(shù)
怎樣變化，總有
為直角？若存在，求出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】數(shù)列
的前
項和為
，若存在正整數(shù)
，且
，使得
，
同時成立，則稱數(shù)列為“
數(shù)列”.
（1）若首項為
，公差為
的等差數(shù)列是“
數(shù)列”，求的值；
（2）已知數(shù)列為等比數(shù)列，公比為
.
①若數(shù)列為“數(shù)列”，
，求的值；
②若數(shù)列為“數(shù)列”，
，求證：
為奇數(shù)，
為偶數(shù).
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在棱長為2的正方體
中，點M是對角線
上的點（點M與A、
不重合），則下列結論正確的個數(shù)為（ ）
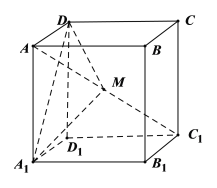
①存在點M，使得平面
平面
；
②存在點M，使得
平面；
③若
的面積為S，則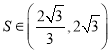
；
④若
、
分別是在平面
與平面
的正投影的面積，則存在點M，使得
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
