
【題目】設D是函數y=f(x)定義域內的一個區(qū)間,若存在x0∈D,使f(x0)=﹣x0 , 則稱x0是f(x)的一個“次不動點”,也稱f(x)在區(qū)間D上存在次不動點.若函數f(x)=ax2﹣3x﹣a+ ![]() 在區(qū)間[1,4]上存在次不動點,則實數a的取值范圍是( )
在區(qū)間[1,4]上存在次不動點,則實數a的取值范圍是( )
A.(﹣∞,0)
B.(0, ![]() )
)
C.[ ![]() ,+∞)
,+∞)
D.(﹣∞, ![]() ]
]
【答案】D
【解析】解:依題意,存在x∈[1,4], 使F(x)=f(x)+x=ax2﹣2x﹣a+ ![]() =0,
=0,
當x=1時,使F(1)= ![]() ≠0;
≠0;
當x≠1時,解得a= ![]() ,
,
∴a′= 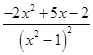 =0,
=0,
得x=2或x= ![]() ,(
,( ![]() <1,舍去),
<1,舍去),
x | (1,2) | 2 | (2,4) |
a′ | + | 0 | ﹣ |
a | ↗ | 最大值 | ↘ |
∴當x=2時,a最大= ![]() =
= ![]() ,
,
所以常數a的取值范圍是(﹣∞, ![]() ],
],
故選:D.
根據“f(x)在區(qū)間D上有次不動點”當且僅當“F(x)=f(x)+x在區(qū)間D上有零點”,依題意,存在x∈[1,4],使F(x)=f(x)+x=ax2﹣2x﹣a+ ![]() =0,討論將a分離出來,利用導數研究出等式另一側函數的取值范圍即可求出a的范圍.
=0,討論將a分離出來,利用導數研究出等式另一側函數的取值范圍即可求出a的范圍.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數 f(x)=1+x﹣ ![]() ,g (x)=1﹣x+
,g (x)=1﹣x+ ![]() ,設函數F(x)=f(x﹣4)g(x+3),且函數 F ( x) 的零點均在區(qū)間[a,b]( a<b,a,b∈Z )內,則 b﹣a 的最小值為 .
,設函數F(x)=f(x﹣4)g(x+3),且函數 F ( x) 的零點均在區(qū)間[a,b]( a<b,a,b∈Z )內,則 b﹣a 的最小值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的可導函數f(x)的導函數為f′(x),滿足f′(x)<f(x),且f(﹣x)=f(2+x),f(2)=1,則不等式f(x)<ex的解集為( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在Rt△ABC中,∠A=90°,點D是邊BC上的動點,且| ![]() |=3,|
|=3,| ![]() |=4,
|=4, ![]() =λ
=λ ![]() +μ
+μ ![]() (λ>0,μ>0),則當λμ取得最大值時,|
(λ>0,μ>0),則當λμ取得最大值時,| ![]() |的值為( )
|的值為( )
A.![]()
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln(x﹣1)+ax2+x+1,g(x)=(x﹣1)ex+ax2 , a∈R. (Ⅰ)當a=1時,求函數f(x)在點(2,f(2))處的切線方程;
(Ⅱ)若函數g(x)有兩個零點,試求a的取值范圍;
(Ⅲ)證明f(x)≤g(x)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1 , F2分別是橢圓C: ![]() =1(a>b>0)的兩個焦點,P(1,
=1(a>b>0)的兩個焦點,P(1, ![]() )是橢圓上一點,且
)是橢圓上一點,且 ![]() |PF1|,|F1F2|,
|PF1|,|F1F2|, ![]() |PF2|成等差數列.
|PF2|成等差數列.
(1)求橢圓C的標準方程;
(2)已知動直線l過點F2 , 且與橢圓C交于A、B兩點,試問x軸上是否存在定點Q,使得 ![]() =﹣
=﹣ ![]() 恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
恒成立?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校開展“讀好書,好讀書”活動,要求本學期每人至少讀一本課外書,該校高一共有100名學生,他們本學期讀課外書的本數統(tǒng)計如圖所示. (Ⅰ)求高一學生讀課外書的人均本數;
(Ⅱ)從高一學生中任意選兩名學生,求他們讀課外書的本數恰好相等的概率;
(Ⅲ)從高一學生中任選兩名學生,用ζ表示這兩人讀課外書的本數之差的絕對值,求隨機變量ζ的分布列及數學期望E.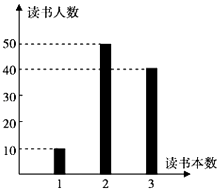
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,三邊a,b,c所對應的角分別是A,B,C,已知a,b,c成等比數列.
(1)若 ![]() +
+ ![]() =
= ![]() ,求角B的值;
,求角B的值;
(2)若△ABC外接圓的面積為4π,求△ABC面積的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com