
如圖,已知橢圓C的中心在原點O,焦點在 軸上,長軸長是短軸
軸上,長軸長是短軸
長的2倍,且經過點M .
平行于OM的直線
.
平行于OM的直線 在
在 軸上的截距為
軸上的截距為
 并交橢
并交橢
圓C于A、B兩個不同點.
(1)求橢圓C的標準方程;
(2)求 的取值范圍;
的取值范圍;
|
 軸始終圍成一個等腰三角形.
軸始終圍成一個等腰三角形.

(1) (2)
(2) (3)見解析
(3)見解析
【解析】本試題主要是考查了橢圓方程的求解以及直線與橢圓的位置關系的總額和運用。
(1)設橢圓C的標準方程為
 (
( >
> >0)
>0)
由題意 ,結合性質得到參數a,b的值
,結合性質得到參數a,b的值
(2)
 設
設 :
: 由
由
聯立方程組,然后根據判別式大于零得到m的范圍。
(3)設 ,則
,則 、
、 為(
為( )式的兩根,
)式的兩根,
設MA交 軸于點P,MB交
軸于點P,MB交 軸于點Q
軸于點Q

 MA的方程為:
MA的方程為:
令 ,可得P(
,可得P( )=
)=
同理得到點Q的坐標,然后結合中點公式,得到并證明。
解:(1)設橢圓C的標準方程為
 (
( >
> >0)
>0)
由題意
解得
 C的方程為
C的方程為 ………………4分
………………4分
(2)
 設
設 :
: 由
由
消去 得
得

 直線
直線 與橢圓有兩個不同的交點
與橢圓有兩個不同的交點

 式有兩個不等實根
式有兩個不等實根
則 >0
>0
解得 <
< <2 又
<2 又
 的取值范圍為
的取值范圍為 ………………8分
………………8分
(3)設 ,則
,則 、
、 為(
為( )式的兩根,
)式的兩根,
設MA交 軸于點P,MB交
軸于點P,MB交 軸于點Q
軸于點Q

 MA的方程為:
MA的方程為:
令 ,可得P(
,可得P( )=
)=
同理可得Q
設PQ的中點為N,則
由②知
又

 MPQ的中線MN
MPQ的中線MN PQ
PQ
 MPQ為等腰三角形 ………………12分
MPQ為等腰三角形 ………………12分
注:其他正確解法請按步驟酌情給分。


科目:高中數學 來源: 題型:
 在平面直角坐標系xOy中,如圖,已知橢圓C:
在平面直角坐標系xOy中,如圖,已知橢圓C:| x2 | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江蘇五校高三下學期期初教學質量調研數學卷(解析版) 題型:解答題
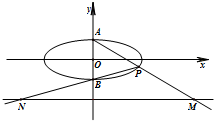
在平面直角坐標系xOy中,如圖,已知橢圓C: 的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、PB與直線l:y=-2分別交于點M、N.
的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、PB與直線l:y=-2分別交于點M、N.

(1)設直線AP、PB的斜率分別為k1,k2,求證:k1·k2為定值;
(2)求線段MN長的最小值;
(3)當點P運動時,以MN為直徑的圓是否經過某定點?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省華南師大附中高三(下)5月月考數學試卷(理科)(解析版) 題型:解答題
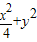 =1的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、BP與直線l:y=-2分別交于點M、N;
=1的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、BP與直線l:y=-2分別交于點M、N;
查看答案和解析>>
科目:高中數學 來源:2012-2013學年廣東省華南師大附中高三(下)5月月考數學試卷(文科)(解析版) 題型:解答題
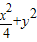 =1的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、BP與直線l:y=-2分別交于點M、N;
=1的上、下頂點分別為A、B,點P在橢圓C上且異于點A、B,直線AP、BP與直線l:y=-2分別交于點M、N;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com