
【題目】已知函數![]() (
(![]() ).
).
(1)若函數![]() 有兩個零點,求實數a的取值范圍
有兩個零點,求實數a的取值范圍
(2)證明:![]()
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)令![]() ,得到
,得到![]() ,令
,令![]() ,
,![]() ,利用導數求得函數
,利用導數求得函數![]() 的單調性與最小值
的單調性與最小值![]() ,要使函數
,要使函數![]() 有兩個零點,則函數
有兩個零點,則函數![]() 的圖象與
的圖象與![]() 有兩個不同的交點,即可求解;
有兩個不同的交點,即可求解;
(2)要證明![]() ,只需
,只需![]() ,令
,令![]() ,利用導數求得函數的
,利用導數求得函數的![]() 的單調性與最值,即可求解.
的單調性與最值,即可求解.
(1)由題意,函數![]() 的定義域為
的定義域為![]() ,
,
令![]() ,則
,則![]() ,
,
記![]() ,
,![]() ,
,
則![]() ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
所以![]() 有最小值,且為
有最小值,且為![]() ,
,
又當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以要使函數![]() 有兩個零點,則函數
有兩個零點,則函數![]() 的圖象與
的圖象與![]() 有兩個不同的交點,
有兩個不同的交點,
則![]() ,即實數a的取值范圍為
,即實數a的取值范圍為![]() .
.
(2)由(1)知,函數![]() 有最小值為
有最小值為![]() ,可得
,可得![]() ,
,
當且僅當![]() 時取等號,
時取等號,
因此要證明![]() ,
,
即只需要證明![]() ,
,
記![]() ,則
,則![]()
![]() ,
,
令![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
所以![]() ,
,
即![]() 恒成立,當且僅當
恒成立,當且僅當![]() 時取等號,
時取等號,
所以![]() ,當且僅當
,當且僅當![]() 時取等號.
時取等號.


科目:高中數學 來源: 題型:
【題目】如圖1,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,過
,過![]() ,
,![]() 分別作
分別作![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() ,
,![]() ,已知
,已知![]() ,
,![]() ,將梯形
,將梯形![]() 沿
沿![]() ,
,![]() 同側折起,使得平面
同側折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,得到圖2.
,得到圖2.
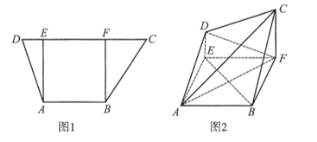
(1)證明:![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某省從1月21日至2月24日的新冠肺炎每日新增確診病例變化曲線圖.

若該省從1月21日至2月24日的新冠肺炎每日新增確診人數按日期順序排列構成數列![]() ,
,![]() 的前n項和為
的前n項和為![]() ,則下列說法中正確的是( )
,則下列說法中正確的是( )
A.數列![]() 是遞增數列B.數列
是遞增數列B.數列![]() 是遞增數列
是遞增數列
C.數列![]() 的最大項是
的最大項是![]() D.數列
D.數列![]() 的最大項是
的最大項是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,A的坐標為(2,0),B是第一象限內的一點,以C為圓心的圓經過OAB三點,且圓C在點A,B處的切線相交于P,若P的坐標為(4,2),則直線PB的方程為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點A1,A2,…,An,…B1,B2,…,Bn,…均在拋物線x=y2上,線段AnBn與x軸的交點為Hn.將△OA1B1,△H1A2B2,…,△HnAn+1Bn+1,…的面積分別記為S1,S2,…,Sn+1,….已知上述三角形均為等腰直角三角形,且它們的頂角分別為O,H1,…,Hn,….
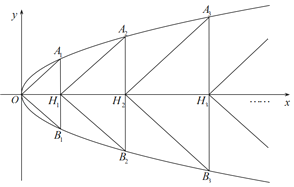
(1)求S1和S2的值;
(2)證明:n≤sn≤n2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是橢圓
是橢圓![]() 的左、右焦點,橢圓的短軸長為
的左、右焦點,橢圓的短軸長為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上的一點,過點
上的一點,過點![]() 作
作![]() 軸的垂線交橢圓于另一點
軸的垂線交橢圓于另一點![]() (
(![]() 不過點
不過點![]() ),且
),且![]() 的周長的最大值為8.
的周長的最大值為8.
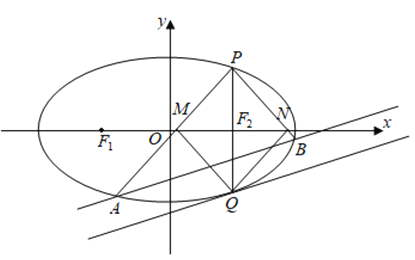
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() 過焦點
過焦點![]() ,在橢圓上取兩點
,在橢圓上取兩點![]() ,連接
,連接![]() ,與
,與![]() 軸的交點分別為
軸的交點分別為![]() ,過點
,過點![]() 作橢圓的切線
作橢圓的切線![]() ,當四邊形
,當四邊形![]() 為菱形時,證明:直線
為菱形時,證明:直線![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種植物感染![]() 病毒極易導致死亡,某生物研究所為此推出了一種抗
病毒極易導致死亡,某生物研究所為此推出了一種抗![]() 病毒的制劑,現對
病毒的制劑,現對![]() 株感染了
株感染了![]() 病毒的該植株樣本進行噴霧試驗測試藥效.測試結果分“植株死亡”和“植株存活”兩個結果進行統計;并對植株吸收制劑的量(單位:
病毒的該植株樣本進行噴霧試驗測試藥效.測試結果分“植株死亡”和“植株存活”兩個結果進行統計;并對植株吸收制劑的量(單位:![]() )進行統計規定:植株吸收在
)進行統計規定:植株吸收在![]() (包括
(包括![]() )以上為“足量”,否則為“不足量”.現對該
)以上為“足量”,否則為“不足量”.現對該![]() 株植株樣本進行統計,其中“植株存活”的
株植株樣本進行統計,其中“植株存活”的![]() 株,對制劑吸收量統計得下表.已知“植株存活”但“制劑吸收不足量”的植株共
株,對制劑吸收量統計得下表.已知“植株存活”但“制劑吸收不足量”的植株共![]() 株.
株.
編號 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
吸收量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)完成以![]() 下列聯表,并判斷是否可以在犯錯誤概率不超過
下列聯表,并判斷是否可以在犯錯誤概率不超過![]() 的前提下,認為“植株的存活”與“制劑吸收足量”有關?
的前提下,認為“植株的存活”與“制劑吸收足量”有關?
吸收足量 | 吸收不足量 | 合計 | |
植株存活 |
| ||
植株死亡 | |||
合計 |
|
(2)若在該樣本“制劑吸收不足量”的植株中隨機抽取![]() 株,求這
株,求這![]() 株中恰有
株中恰有![]() 株“植株存活”的概率.
株“植株存活”的概率.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
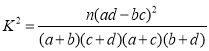 ,其中
,其中![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com