
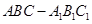 中,側棱
中,側棱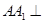 底面
底面 ,
,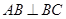 ,
,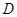 為
為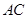 的中點,
的中點,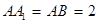 .
.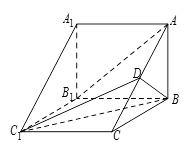
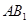 //平面
//平面 ;
;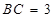 ,求四棱錐
,求四棱錐 的體積.
的體積.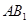 //平面
//平面 ,需要在平面
,需要在平面 內找一條與
內找一條與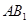 平行的直線,而要找這條直線一般通過作過
平行的直線,而要找這條直線一般通過作過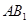 且與平面
且與平面 相交的平面來找.在本題中聯系到
相交的平面來找.在本題中聯系到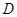 為
為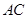 中點,故連結
中點,故連結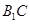 ,這樣便得一平面
,這樣便得一平面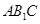 ,接下來只需證
,接下來只需證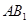 與平面
與平面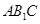 和平面
和平面 的交線平行即可.
的交線平行即可. 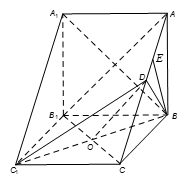
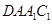 為一直角梯形,故易得其面積,本題的關鍵是求出點B到平面
為一直角梯形,故易得其面積,本題的關鍵是求出點B到平面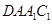 的距離.由于
的距離.由于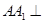 平面
平面 ,所以易得平面
,所以易得平面
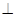 平面
平面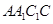 .平面
.平面
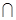 平面
平面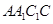
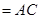 .根據兩平面垂直的性質定理知,只需過B作交線AC的垂線即可得點B到平面
.根據兩平面垂直的性質定理知,只需過B作交線AC的垂線即可得點B到平面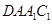 的距離,從而求出體積.
的距離,從而求出體積.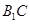 ,設
,設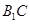 與
與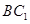 相交于點
相交于點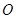 ,連接
,連接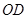 ,
,
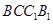 是平行四邊形,
是平行四邊形,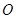 為
為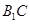 的中點.
的中點.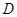 為
為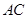 的中點,∴
的中點,∴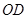 為△
為△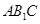 的中位線,
的中位線,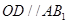 .
.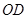
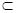 平面
平面 ,
,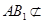 平面
平面 ,
,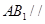 平面
平面 . 6分
. 6分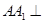 平面
平面 ,
,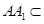 平面
平面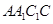 ,
,
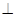 平面
平面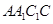 ,且平面
,且平面
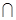 平面
平面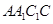
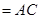 .
.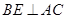 ,垂足為
,垂足為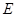 ,則
,則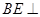 平面
平面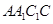 ,
, 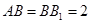 ,
,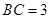 ,
, 中,
中,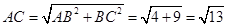 ,
,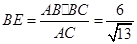 ,
,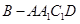 的體積
的體積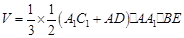
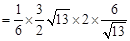
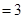 12分
12分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com