
【題目】函數![]() 的定義域為
的定義域為![]() ,且
,且![]() ,當
,當![]() 時,
時,![]() ,
,![]() .
.
(1)求![]() 和
和![]() ;
;
(2)證明函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(3)求不等式![]() 的解集.
的解集.
【答案】(1)f(1)=0,f(9)=2(2)證明見解析(3)(8,9)
【解析】
(1)賦值法求![]() 和
和![]() ,令
,令![]() ,求出
,求出![]() ;再令
;再令![]() ,結合已知,可求
,結合已知,可求![]() ,再令
,再令![]() ,即可求解;
,即可求解;
(2)設![]() ,由
,由![]() 結合已知,可證
結合已知,可證![]() ,即可得出結論;
,即可得出結論;
(3)由(1)結合已知,不等式可化為![]() ,根據函數的單調性和定義域,轉化為關于
,根據函數的單調性和定義域,轉化為關于![]() 的不等式組,即可求出結論.
的不等式組,即可求出結論.
(1)令x=y=1,則f(1)=f(1)+f(1),即f(1)=0,
令x=3,y![]() ,則f(3
,則f(3![]() )=f(3)+f(
)=f(3)+f(![]() )=f(1)=0,
)=f(1)=0,
即![]() ,則
,則![]() ,
,
令x=3,y=3得![]() .
.
(2)設![]() ,則
,則![]() ,則
,則![]() ,
,
則f(x1)=f(x2![]() )=f(x2)+f(
)=f(x2)+f(![]() )>f(x2),
)>f(x2),
即函數f(x)在(0,+∞)上為增函數.
(3)不等式f(x)+f(x﹣8)<2等價為![]() ,
,
則等價為 ,得
,得 得8<x<9,
得8<x<9,
即不等式的解集為(8,9).


科目:高中數學 來源: 題型:
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜.過去50周的資料顯示,該地周光照量![]() (小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量
(小時)都在30小時以上,其中不足50小時的周數有5周,不低于50小時且不超過70小時的周數有35周,超過70小時的周數有10周.根據統計,該基地的西紅柿增加量![]() (百斤)與使用某種液體肥料
(百斤)與使用某種液體肥料![]() (千克)之間對應數據為如圖所示的折線圖.
(千克)之間對應數據為如圖所示的折線圖.

(1)依據數據的折線圖,是否可用線性回歸模型擬合![]() 與
與![]() 的關系?請計算相關系數
的關系?請計算相關系數![]() 并加以說明(精確到0.01).(若
并加以說明(精確到0.01).(若![]() ,則線性相關程度很高,可用線性回歸模型擬合)
,則線性相關程度很高,可用線性回歸模型擬合)
(2)蔬菜大棚對光照要求較大,某光照控制儀商家為該基地提供了部分光照控制儀,但每周光照控制儀最多可運行臺數受周光照量![]() 限制,并有如下關系:
限制,并有如下關系:
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行,則該臺光照控制儀周利潤為3000元;若某臺光照控制儀未運行,則該臺光照控制儀周虧損1000元.若商家安裝了3臺光照控制儀,求商家在過去50周周總利潤的平均值.
附:相關系數公式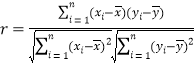 ,參考數據
,參考數據![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出定義:若![]() (其中m為整數),則m叫做與實數x”親密的整數”記作{x}=m,在此基礎上給出下列關于函數
(其中m為整數),則m叫做與實數x”親密的整數”記作{x}=m,在此基礎上給出下列關于函數![]() 的四個說法:
的四個說法:
①函數![]() 在
在![]() 是增函數;
是增函數;
②函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
③函數![]() 在
在![]() 上單調遞增
上單調遞增
④當![]() 時,函數
時,函數![]() 有兩個零點,
有兩個零點,
其中說法正確的序號是( )
A.①②③B.②③④C.①②④D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}的前n項和為Sn,已知an>0,an2+2an=4Sn+3.
(1)求a1的值;
(2)求{an}的通項公式:
(3)設bn=![]() ,求數列{bn}的前n項和.
,求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市效外景區內一條筆直的公路經過三個景點A、B、C.景區管委會又開發了風景優美的景點D.經測量景點D位于景點A的北偏東30°方向且距A 8 km處,且位于景點B的正北方向,還位于景點C的北偏西75°方向 上,已知AB=5 km,AD>BD.
(1)景區管委會準備由景點D向景點B修建一條筆直的公路,不考慮其他因素,求出這條公路的長;
(2)求∠ACD的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直二面角D—AB—E中,四邊形ABCD是邊長為2的正方形,AE=EB,F為CE上的點,且BF⊥平面ACE.

(Ⅰ)求證AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
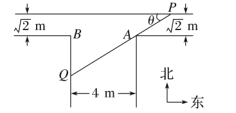
【題目】某“![]() ” 型水渠南北向寬為
” 型水渠南北向寬為![]() ,東西向寬為
,東西向寬為![]() ,其俯視圖如圖所示.假設水渠內的水面始終保持水平位置.
,其俯視圖如圖所示.假設水渠內的水面始終保持水平位置.
(1) 過點![]() 的一條直線與水渠的內壁交于
的一條直線與水渠的內壁交于![]() 兩點,且與水渠的一邊的夾角為
兩點,且與水渠的一邊的夾角為![]() (
(![]() 為銳角),將線段
為銳角),將線段![]() 的長度
的長度![]() 表示為
表示為![]() 的函數;
的函數;
(2) 若從南面漂來一根長度為![]() 的筆直的竹竿(粗細不計),竹竿始終浮于水平面內,且不發生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?試說明理由.
的筆直的竹竿(粗細不計),竹竿始終浮于水平面內,且不發生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com