
在平面直角坐標系中,已知向量![]() (
(![]() ),
),![]() ,動點
,動點![]() 的軌跡為T.
的軌跡為T.
(1)求軌跡T的方程,并說明該方程表示的曲線的形狀;
(2)當![]() 時,已知
時,已知![]() 、
、![]() ,試探究是否存在這樣的點
,試探究是否存在這樣的點![]() :
: ![]() 是軌跡T內部的整點(平面內橫、縱坐標均為整數的點稱為整點),且△OEQ的面積
是軌跡T內部的整點(平面內橫、縱坐標均為整數的點稱為整點),且△OEQ的面積![]() ?若存在,求出點Q的坐標,若不存在,說明理由.
?若存在,求出點Q的坐標,若不存在,說明理由.
(1)軌跡方程為:![]()
當![]() 時,方程表示兩條與x軸平行的直線;
時,方程表示兩條與x軸平行的直線;
當![]() 時,方程表示以原點為圓心,4為半徑的圓;
時,方程表示以原點為圓心,4為半徑的圓;
當![]() 且
且![]() 時,方程表示橢圓;
時,方程表示橢圓;
當![]() 時,方程表示雙曲線.
時,方程表示雙曲線.
(2)滿足條件的點![]() 存在,共有6個,它們的坐標分別為:
存在,共有6個,它們的坐標分別為:
![]()
![]()
(1)∵![]() ∴
∴![]()
![]() 得
得![]() 即
即![]() ------------------------------------2分
------------------------------------2分
當![]() 時,方程表示兩條與x軸平行的直線;(答方程表示兩條直線不扣分)----------------------------3分
時,方程表示兩條與x軸平行的直線;(答方程表示兩條直線不扣分)----------------------------3分
當![]() 時,方程表示以原點為圓心,4為半徑的圓;(答方程表示圓不扣分)-----------------------4分
時,方程表示以原點為圓心,4為半徑的圓;(答方程表示圓不扣分)-----------------------4分
當![]() 且
且![]() 時,方程表示橢圓;-------------------------------------5分
時,方程表示橢圓;-------------------------------------5分
當![]() 時,方程表示雙曲線.-------------------------------------------6分
時,方程表示雙曲線.-------------------------------------------6分
(2)由(1)知,當![]() 時,軌跡T的方程為:
時,軌跡T的方程為:![]() .
.
連結OE,易知軌跡T上有兩個點A![]() ,B
,B![]() 滿足
滿足![]() ,
,
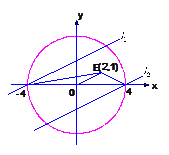 分別過A、B作直線OE的兩條平行線
分別過A、B作直線OE的兩條平行線![]() 、
、![]() .
.
∵同底等高的兩個三角形的面積相等
∴符合條件的點均在直線![]() 、
、![]() 上. --------------------------------7分
上. --------------------------------7分
∵![]() ∴直線
∴直線![]() 、
、![]() 的方程分別為:
的方程分別為:![]() 、
、![]() --------8分
--------8分
設點![]() (
(![]() )∵
)∵![]() 在軌跡T內,∴
在軌跡T內,∴![]() -----------------------9分
-----------------------9分
分別解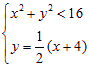 與
與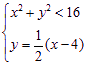 得
得![]() 與
與![]()
∵![]() ∴
∴![]() 為偶數,在
為偶數,在![]() 上
上![]() ,對應的
,對應的![]()
在![]() 上
上![]() ,對應的
,對應的![]() -----------------------13分
-----------------------13分
∴滿足條件的點![]() 存在,共有6個,它們的坐標分別為:
存在,共有6個,它們的坐標分別為:
![]()
![]() .------------------------------------------14分
.------------------------------------------14分


科目:高中數學 來源: 題型:
| π | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com