設(shè)等差數(shù)列
的前
項(xiàng)和為
，則
，
，
，
成等差數(shù)列．類比
以上結(jié)論有：設(shè)等比數(shù)列
的前項(xiàng)積為
，則
， ，
成等比數(shù)列．
學(xué)習(xí)實(shí)踐園地系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題
給出四個(gè)等式：
1＝1
1－4＝－(1＋2)
1－4＋9＝1＋2＋3
1－4＋9－16＝－(1＋2＋3＋4)
……
（1）寫出第5,6個(gè)等式，并猜測(cè)第n(n∈N*)個(gè)等式
（2）用數(shù)學(xué)歸納法證明你猜測(cè)的等式．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：解答題
已知數(shù)列{bn}是等差數(shù)列，b1＝1，b1＋b2＋…＋b10＝145.
(1)求數(shù)列{bn}的通項(xiàng)公式bn；
(2)設(shè)數(shù)列{an}的通項(xiàng)an＝loga
(其中a＞0且a≠1)．記Sn是數(shù)列{an}的前n項(xiàng)和，試比較Sn與
logabn＋1的大小，并證明你的結(jié)論.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
等差數(shù)列有如下性質(zhì)：若數(shù)列
為等差數(shù)列，則當(dāng)
時(shí)，數(shù)列
也是等差數(shù)列；類比上述性質(zhì)，相應(yīng)地，若數(shù)列
是正項(xiàng)等比數(shù)列，當(dāng)
_ 時(shí)，
數(shù)列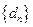
也是等比數(shù)列．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
在解決問(wèn)題：“證明數(shù)集
沒(méi)有最小數(shù)”時(shí)，可用反證法證明．
假設(shè)
是
中的最小數(shù)，則取
，可得：
，與假設(shè)中“
是中的最小數(shù)”矛盾！那么對(duì)于問(wèn)題：“證明數(shù)集
沒(méi)有最大數(shù)”，也可以用反證法證明．我們可以假設(shè)
是
中的最大數(shù)，則可以找到
▲ （用
，
表示），由此可知
，
，這與假設(shè)矛盾！所以數(shù)集沒(méi)有最大數(shù)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
“無(wú)理數(shù)是無(wú)限小數(shù)，而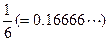
是無(wú)限小數(shù)，所以
是無(wú)理數(shù)。”
這個(gè)推理是 _推理（在“歸納”、“類比”、“演繹”中選擇填空）
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：填空題
已知
，
,
，
，則第5個(gè)等式為 ，…,推廣到第
個(gè)等式為__ _；（注意：按規(guī)律寫出等式的形式，不要求計(jì)算結(jié)果．）
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
≤
.