
【題目】如圖,在四棱錐P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分)
(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,且四棱錐P﹣ABCD的體積為 ![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
【答案】
(1)
證明:∵在四棱錐P﹣ABCD中,∠BAP=∠CDP=90°,
∴AB⊥PA,CD⊥PD,
又AB∥CD,∴AB⊥PD,
∵PA∩PD=P,∴AB⊥平面PAD,
∵AB平面PAB,∴平面PAB⊥平面PAD.
(2)
解:設PA=PD=AB=DC=a,取AD中點O,連結PO,
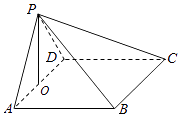
∵PA=PD=AB=DC,∠APD=90°,平面PAB⊥平面PAD,
∴PO⊥底面ABCD,且AD= ![]() =
= ![]() ,PO=
,PO= ![]() ,
,
∵四棱錐P﹣ABCD的體積為 ![]() ,
,
∴VP﹣ABCD= ![]()
= ![]() =
= ![]() =
= ![]() =8,
=8,
解得a=2,∴PA=PD=AB=DC=2,AD=BC=2 ![]() ,PO=
,PO= ![]() ,
,
∴PB=PC= ![]() =2
=2 ![]() ,
,
∴該四棱錐的側面積:
S側=S△PAD+S△PAB+S△PDC+S△PBC
= ![]() +
+ ![]() +
+ ![]() +
+ ![]()
= ![]()
=6+2 ![]() .
.
【解析】(1.)推導出AB⊥PA,CD⊥PD,從而AB⊥PD,進而AB⊥平面PAD,由此能證明平面PAB⊥平面PAD.
(2.)設PA=PD=AB=DC=a,取AD中點O,連結PO,則PO⊥底面ABCD,且AD= ![]() ,PO=
,PO= ![]() ,由四棱錐P﹣ABCD的體積為
,由四棱錐P﹣ABCD的體積為 ![]() ,求出a=2,由此能求出該四棱錐的側面積.
,求出a=2,由此能求出該四棱錐的側面積.
【考點精析】關于本題考查的平面與平面垂直的判定,需要了解一個平面過另一個平面的垂線,則這兩個平面垂直才能得出正確答案.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
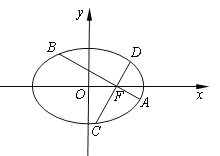
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的離心率為
的離心率為![]() ,過橢圓右焦點
,過橢圓右焦點![]() 作兩條互相垂直的弦
作兩條互相垂直的弦![]() 與
與![]() .當直線
.當直線![]() 斜率為0時,
斜率為0時,![]() .
.
(1)求橢圓的方程;
(2)求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x<2},B={x|3﹣2x>0},則( )
A.A∩B={x|x< ![]() }
}
B.A∩B=?
C.A∪B={x|x< ![]() }
}
D.AUB=R
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,函數
,函數![]() ,
,
![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若![]() 的最小值為
的最小值為![]() ,求實數
,求實數![]() 的值;
的值;
(3)是否存在實數![]() ,使函數
,使函數![]() ,
,![]() 有四個不同的零點?若存在,求出
有四個不同的零點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學名著《算法統宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數是上一層燈數的2倍,則塔的頂層共有燈( )
A.1盞
B.3盞
C.5盞
D.9盞
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC= ![]() AD,∠BAD=∠ABC=90°,E是PD的中點.
AD,∠BAD=∠ABC=90°,E是PD的中點.
(Ⅰ)證明:直線CE∥平面PAB;
(Ⅱ)點M在棱PC 上,且直線BM與底面ABCD所成角為45°,求二面角M﹣AB﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(x﹣1)﹣kx+k+1.
(1)當k=1時,證明:f(x)≤0;
(2)求函數f(x)的單調區間;
(3)證明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() (n∈N* , 且n≥2).
(n∈N* , 且n≥2).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com