

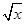 ;
;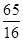 萬元.
萬元.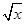 ,由0.25=k1x1得:k1="0.25," y=k2
,由0.25=k1x1得:k1="0.25," y=k2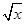 ,由2.5=k2
,由2.5=k2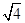 得k2=1.25.
得k2=1.25.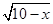 ,得到了y關于x的函數關系式,為了方便求最值,利用換元的方法令
,得到了y關于x的函數關系式,為了方便求最值,利用換元的方法令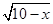 =t(0≤t≤10),
=t(0≤t≤10),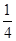 [-(t-
[-(t-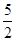 )2+
)2+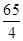 ],這樣就轉化為二次函數求最值問題.
],這樣就轉化為二次函數求最值問題.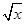 ,由2.5=k2
,由2.5=k2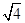 得k2=1.25
得k2=1.25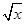 ……………………………………4分
……………………………………4分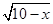 ……………………………………6分
……………………………………6分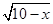 =t(0≤t≤10)則
=t(0≤t≤10)則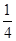 (10-t2)+
(10-t2)+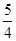 t=
t=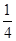 (-t2+5t+10)
(-t2+5t+10)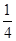 [-(t-
[-(t-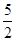 )2+
)2+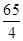 ]……………………………………8分
]……………………………………8分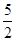 時,y取得最大值
時,y取得最大值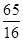 萬元,此時x=3.75萬元
萬元,此時x=3.75萬元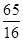 萬元.
萬元.

 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:高中數學 來源:不詳 題型:解答題
 ,
, 
 在
在 上是減函數,求實數
上是減函數,求實數 的取值范圍;
的取值范圍; ,是否存在實數
,是否存在實數 ,當
,當
 (
( 是自然常數)時,函數
是自然常數)時,函數 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,說明理由;
的值;若不存在,說明理由;
 時,證明:
時,證明: 
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 (萬元)與年產量
(萬元)與年產量 (噸)之間的關系可近似地表示為
(噸)之間的關系可近似地表示為
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com