
【題目】如圖,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點,
的中點,![]() 為棱
為棱![]() 上的一點,且
上的一點,且![]() //平面
//平面![]() .
.
(1)求![]() 的值;
的值;
(2)求證:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
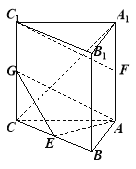
【答案】(1)![]() ;(2)詳見解析;(3)二面角
;(2)詳見解析;(3)二面角![]() 的余弦值為
的余弦值為![]() .
.
【解析】
試題分析:(1)求![]() 的值,關(guān)鍵是找
的值,關(guān)鍵是找![]() 在
在![]() 的位置,注意到
的位置,注意到![]() 平面
平面![]() ,有線面平行的性質(zhì),可得
,有線面平行的性質(zhì),可得![]() ,由已知
,由已知![]() 為
為![]() 中點,由平面幾何知識可得
中點,由平面幾何知識可得![]() 為
為![]() 中點,從而可得
中點,從而可得![]() 的值;(2)求證:
的值;(2)求證:![]() ,有圖觀察,用傳統(tǒng)方法比較麻煩,而本題由于
,有圖觀察,用傳統(tǒng)方法比較麻煩,而本題由于![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,這樣建立空間坐標比較簡單,故以
,這樣建立空間坐標比較簡單,故以![]() 為原點,以
為原點,以![]() 分別為
分別為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系![]() ,取
,取![]() ,可寫出個點坐標,從而得向量
,可寫出個點坐標,從而得向量![]() 的坐標,證
的坐標,證![]() 即可;(3)求二面角
即可;(3)求二面角![]() 的余弦值,由題意可得向量
的余弦值,由題意可得向量![]() 是平面
是平面![]() 的一個法向量,只需求出平面
的一個法向量,只需求出平面![]() 的一個法向量,可設平面
的一個法向量,可設平面![]() 的法向量
的法向量![]() ,利用
,利用 ,即可求出平面
,即可求出平面![]() 的一個法向量,利用向量的夾角公式即可求出二面角
的一個法向量,利用向量的夾角公式即可求出二面角![]() 的余弦值.
的余弦值.
(1)因為![]() 平面
平面![]()
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() . 3分
. 3分
因為![]() 為
為![]() 中點,且側(cè)面
中點,且側(cè)面![]() 為平行四邊形
為平行四邊形
所以![]() 為
為![]() 中點,所以
中點,所以![]() . 4分
. 4分
(2)因為![]() 底面
底面![]() ,
,
所以![]() ,
,![]() , 5分
, 5分
又![]() ,
,
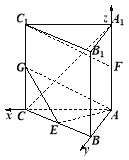
如圖,以![]() 為原點建立空間直角坐標系
為原點建立空間直角坐標系![]() ,設
,設![]() ,則由
,則由![]() 可得
可得![]() 6分
6分
因為![]() 分別是
分別是![]() 的中點,
的中點,
所以![]() . 7分
. 7分
![]() . 8分
. 8分
所以![]() ,
,
所以![]() . 9分
. 9分
(3)設平面![]() 的法向量
的法向量![]() ,則
,則
 即
即![]() 10分
10分
令![]() ,則
,則![]() ,所以
,所以![]() . 11分
. 11分
由已知可得平面![]() 的法向量
的法向量![]() 11分
11分
所以![]() 13分
13分
由題意知二面角![]() 為鈍角,
為鈍角,
所以二面角![]() 的余弦值為
的余弦值為![]() . 14分
. 14分


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若對于任意![]() 都有
都有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)若過點![]() 可作函數(shù)
可作函數(shù)![]() 圖象的三條不同切線,求實數(shù)
圖象的三條不同切線,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設S是實數(shù)集R的非空子集,若對任意x,y∈S,都有x+y,x-y,xy∈S,則稱S為封閉集.下列命題:①集合S={a+b![]() |a,b為整數(shù)}為封閉集;②若S為封閉集,則一定有0∈S;③封閉集一定是無限集;④若S為封閉集,則滿足STR的任意集合T也是封閉集.其中真命題是________.(寫出所有真命題的序號)
|a,b為整數(shù)}為封閉集;②若S為封閉集,則一定有0∈S;③封閉集一定是無限集;④若S為封閉集,則滿足STR的任意集合T也是封閉集.其中真命題是________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(Ⅱ)證明當![]() 時,
時, ![]() ;
;
(Ⅲ)若關(guān)于![]() 的不等式
的不等式![]() 恒成立,求整數(shù)
恒成立,求整數(shù)![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() 是定義在
是定義在![]() 上的偶函數(shù),
上的偶函數(shù), ![]() ,都有
,都有![]() ,且當
,且當![]() 時,
時, ![]() ,若函數(shù)
,若函數(shù)![]() (
(![]() )在區(qū)間
)在區(qū)間![]() 內(nèi)恰有三個不同零點,則實數(shù)
內(nèi)恰有三個不同零點,則實數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】據(jù)中國日報網(wǎng)報道:2017年11月13日,TOP500發(fā)布的最新一期全球超級計算機500強榜單顯示,中國超算在前五名中占據(jù)兩席,其中超算全球第一“神威太湖之光”完全使用了國產(chǎn)品牌處理器。為了了解國產(chǎn)品牌處理器打開文件的速度,某調(diào)查公司對兩種國產(chǎn)品牌處理器進行了12次測試,結(jié)果如下(數(shù)值越小,速度越快,單位是MIPS)
測試1 | 測試2 | 測試3 | 測試4 | 測試5 | 測試6 | 測試7 | 測試8 | 測試9 | 測試10 | 測試11 | 測試12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
(Ⅰ)從品牌A的12次測試中,隨機抽取一次,求測試結(jié)果小于7的概率;
(Ⅱ)從12次測試中,隨機抽取三次,記X為品牌A的測試結(jié)果大于品牌B的測試結(jié)果的次數(shù),求X的分布列和數(shù)學期望E(X);
(Ⅲ)經(jīng)過了解,前6次測試是打開含有文字和表格的文件,后6次測試是打開含有文字和圖片的文件.請你依據(jù)表中數(shù)據(jù),運用所學的統(tǒng)計知識,對這兩種國產(chǎn)品牌處理器打開文件的速度進行評價.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知表1和表2是某年部分日期的天安門廣場升旗時刻表:
表1:某年部分日期的天安門廣場升旗時刻表
日期 | 升旗時刻 | 日期 | 升旗時刻 | 日期 | 升旗時刻 | 日期 | 升旗時刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:11 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:50 | 12月20日 | 7:31 |
表2:某年1月部分日期的天安門廣場升旗時刻表
日期 | 升旗時刻 | 日期 | 升旗時刻 | 日期 | 升旗時刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(1)從表1的日期中隨機選出一天,試估計這一天的升旗時刻早于7:00的概率;
(2)甲、乙二人各自從表2的日期中隨機選擇一天觀看升旗,且兩人的選擇相互獨立,記![]() 為這兩人中觀看升旗的時刻早于7:00的人數(shù),求
為這兩人中觀看升旗的時刻早于7:00的人數(shù),求![]() 的 分布列和數(shù)學期望;
的 分布列和數(shù)學期望;
(3)將表1和表2的升旗時刻化為分數(shù)后作為樣本數(shù)據(jù)(如7:31化為![]() ),記表2中所有升旗時刻對應數(shù)據(jù)的方差為
),記表2中所有升旗時刻對應數(shù)據(jù)的方差為![]() ,表1和表2中所有升旗時刻對應數(shù)據(jù)的方差為
,表1和表2中所有升旗時刻對應數(shù)據(jù)的方差為![]() ,判斷
,判斷![]() 與
與![]() 的大小(只需寫出結(jié)論).
的大小(只需寫出結(jié)論).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com