
【題目】在極坐標系中,曲線 ![]() 的極坐標方程分別為
的極坐標方程分別為 ![]() ,
, ![]() .
.
(1)求曲線 ![]() 和
和 ![]() 的公共點的個數;
的公共點的個數;
(2)過極點作動直線與曲線 ![]() 相交于點Q,在OQ上取一點P,使
相交于點Q,在OQ上取一點P,使 ![]()
![]() ,求點P的軌跡,并指出軌跡是什么圖形.
,求點P的軌跡,并指出軌跡是什么圖形.
【答案】
(1)解: ![]() 的直角坐標方程為
的直角坐標方程為 ![]() ,它表示圓心為
,它表示圓心為 ![]() ,半徑為1的圓,
,半徑為1的圓, ![]() 的直角坐標方程為
的直角坐標方程為 ![]() ,所以曲線
,所以曲線 ![]() 為直線,由于圓心到直線的距離為
為直線,由于圓心到直線的距離為 ![]() ,所以直線與圓相離,即曲線
,所以直線與圓相離,即曲線 ![]() 和
和 ![]() 的公共點個數為0
的公共點個數為0
(2)解:設 ![]() ,
, ![]() ,則
,則 ![]() 即
即 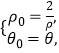 ①
①
因為點 ![]() 在曲線
在曲線 ![]() 上,所以
上,所以 ![]() ,②
,②
將①代入②,得 ![]() ,即
,即 ![]() ,此即為點P的軌跡方程,化為直角坐標方程為
,此即為點P的軌跡方程,化為直角坐標方程為 ![]() ,
,
因此,點P的軌跡是以 ![]() 為圓心,1為半徑的圓
為圓心,1為半徑的圓
【解析】1.根據ρ sin θ = y、ρ cos θ = x、.ρ2=x 2 + y 2化解出直角坐標方程;2.![]() 根據圓心到直線的距離與圓的半徑比較確定直線與圓的位置關系即可得出答案;3.根據已知條件列出關系式,再根據C 2的極坐標方程確定點P的軌跡方程,最后根據P的極坐標方程轉化為直角坐標方程確定軌跡圖形。
根據圓心到直線的距離與圓的半徑比較確定直線與圓的位置關系即可得出答案;3.根據已知條件列出關系式,再根據C 2的極坐標方程確定點P的軌跡方程,最后根據P的極坐標方程轉化為直角坐標方程確定軌跡圖形。


 口算能手系列答案
口算能手系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,在正方體ABCD-A1B1C1D1中,M,N分別為棱C1D1,C1C的中點,有以下四個結論:
①直線AM與CC1是相交直線;②直線AM與BN是平行直線;
③直線BN與MB1是異面直線; ④直線MN與AC所成的角為60°.
其中正確的結論為___ (注:把你認為正確的結論序號都填上).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機調查詢問110名性別不同的高中生是否愛好某項運動,得到如下的列聯表:
男 | 女 | 總計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由 ![]() 計算得
計算得 ![]()
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
參照附表,得到的正確結論是( )
A.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
B.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
C.有99%以上的把握認為“愛好該項運動與性別無關”
D.有99%以上的把握認為“愛好該項運動與性別有關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() .
.
(1)當 ![]() 時,求
時,求 ![]() 的單調區間;
的單調區間;
(2)設 ![]() ,
, ![]() 是曲線
是曲線 ![]() 圖象上的兩個相異的點,若直線
圖象上的兩個相異的點,若直線 ![]() 的斜率
的斜率 ![]() 恒成立,求實數
恒成立,求實數 ![]() 的取值范圍;
的取值范圍;
(3)設函數 ![]() 有兩個極值點
有兩個極值點 ![]() ,
, ![]() ,且
,且 ![]() ,若
,若 ![]() 恒成立,求實數
恒成立,求實數 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標中,直線l的方程為 ![]() ,曲線C的方程為
,曲線C的方程為 ![]() .
.
(1)求直線l與極軸的交點到極點的距離;
(2)若曲線C上恰好有兩個點到直線l的距離為 ![]() ,求實數m的取值范圍.
,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|,其中a>1
(1)當a=2時,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知關于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD為直角梯形,∠ABC=∠BAD=90°,![]() ,
,![]() ,F分別為AB,PC的中點.
,F分別為AB,PC的中點.
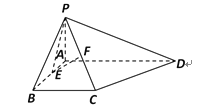
(I)若四棱錐P-ABCD的體積為4,求PA的長;
(II)求證:PE⊥BC;
(III)求PC與平面PAD所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人參加普法知識競賽,共有5個不同題目,選擇題3個,判斷題2個,甲、乙兩人各抽一題.
(1)求甲抽到判斷題,乙抽到選擇題的概率是多少;
(2)求甲、乙兩人中至少有一人抽到選擇題的概率是多少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com