
如圖,在長方體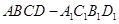 中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱
中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱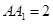 ,
, 為
為 中點,
中點, 為
為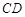 中點,
中點, 為
為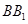 上一個動點.
上一個動點.
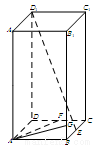
(Ⅰ)確定 點的位置,使得
點的位置,使得 ;
;
(Ⅱ)當(dāng) 時,求二面角
時,求二面角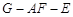 的平面角余弦值.
的平面角余弦值.
(Ⅰ)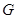 為
為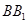 的四等分點;(Ⅱ)
的四等分點;(Ⅱ)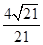 .
.
【解析】
試題分析:(Ⅰ)用向量法的解題步驟是建立恰當(dāng)?shù)目臻g直角坐標(biāo)系,寫出相應(yīng)的點的坐標(biāo)及向量的坐標(biāo),利用向量的數(shù)量積為0,則這兩個向量垂直,得出結(jié)論;(Ⅱ)二面角的問題,找到兩個平面的法向量的夾角,利用向量的夾角公式求解.
試題解析:方法一:
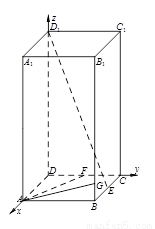
(Ⅰ)如圖,分別以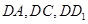 所在直線為
所在直線為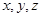 軸建立空間直角坐標(biāo)系
軸建立空間直角坐標(biāo)系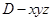 ,則
,則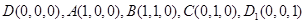
易得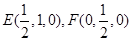 2分
2分
由題意得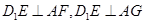 ,設(shè)
,設(shè)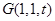
又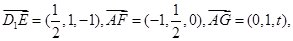
則由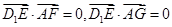 得
得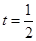 ,
,
∴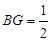 ,得
,得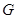 為
為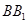 的四等分點.
6分
的四等分點.
6分
(Ⅱ)易知平面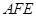 的一個法向量為
的一個法向量為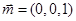 ,設(shè)平面
,設(shè)平面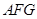 的法向量為
的法向量為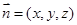
則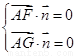 ,得
,得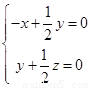 ,取
,取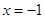 ,得
,得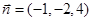 , 10分
, 10分
∴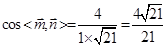 ,∴二面角
,∴二面角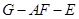 的平面角余弦值為
的平面角余弦值為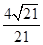 .12分
.12分
方法二:
(Ⅰ)∵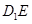 在平面
在平面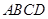 內(nèi)的射影為
內(nèi)的射影為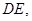 ,且四邊形
,且四邊形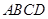 為正方形,
為正方形,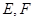 為中點, ∴
為中點, ∴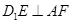
同理,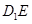 在平面
在平面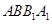 內(nèi)的射影為
內(nèi)的射影為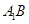 ,則
,則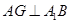
由△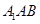 ~△
~△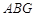 , ∴
, ∴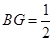 ,得
,得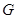 為
為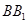 的四等分點.
6分
的四等分點.
6分
(Ⅱ)∵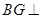 平面
平面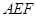 ,過
,過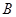 點作
點作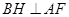 ,垂足為
,垂足為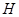 ;
;
連結(jié)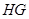 ,則
,則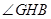 為二面角
為二面角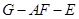 的平面角;
8分
的平面角;
8分
由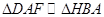 ,得
,得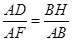 ,解得
,解得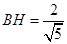
∴在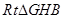 中,
中,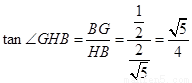 ,
,
∴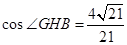 ;∴二面角
;∴二面角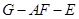 的平面角余弦值為
的平面角余弦值為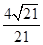 .
12分
.
12分
考點:線面垂直的判定定理,二面角,線面成角的計算.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
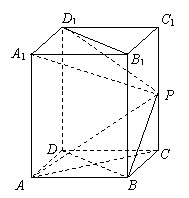 (本小題滿分12分)如圖,在長方體
(本小題滿分12分)如圖,在長方體![]() 中,已知底面ABCD是邊長為1的正方形,側(cè)棱
中,已知底面ABCD是邊長為1的正方形,側(cè)棱![]() ,P是側(cè)棱
,P是側(cè)棱![]() 上的一點,
上的一點,![]() .
.
(Ⅰ)試問直線![]() 與AP能否垂直?并說明理由;
與AP能否垂直?并說明理由;
(Ⅱ)試確定m,使直線AP與平面BDD1B1所成角為60º;
(Ⅲ)若m=1,求平面PA1D1與平面PAB所成角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年湖北省八市高三3月聯(lián)考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分12分)如圖,在長方體 中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱
中,已知上下兩底面為正方形,且邊長均為1;側(cè)棱 ,為
,為 中點,
中點, 為
為 中點,
中點, 為
為 上一個動點.
上一個動點.

(Ⅰ)確定 點的位置,使得
點的位置,使得 ;
;
(Ⅱ)當(dāng) 時,求二面角
時,求二面角 的平
的平
面角余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆江蘇省高二下學(xué)期期中考試?yán)砜茢?shù)學(xué)試卷(解析版) 題型:解答題
如圖,在長方體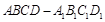 中,已知
中,已知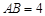 ,
,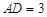 ,
,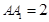 ,E,F(xiàn)分別是棱AB,BC 上的點,且
,E,F(xiàn)分別是棱AB,BC 上的點,且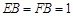 .
.

(1)求異面直線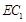 與
與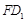 所成角的余弦值;
所成角的余弦值;
(2)試在面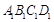 上確定一點G,使
上確定一點G,使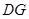
 平面
平面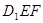 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:銀川二中2010屆高三下學(xué)期第二次模擬考試(理) 題型:解答題
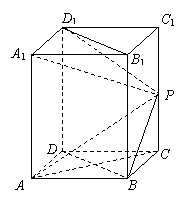 如圖,在長方體
如圖,在長方體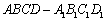
中,已知底面ABCD是邊長為1的正方形,側(cè)棱
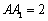 ,P是側(cè)棱
,P是側(cè)棱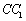 上的一點,
上的一點,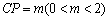 .
.
(Ⅰ)試問直線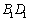 與AP能否垂直?并說明理由;
與AP能否垂直?并說明理由;
(Ⅱ)試確定m,使直線AP與平面BDD1B1所成角為60º;
(Ⅲ)若m=1,求平面PA1D1與平面PAB所成角的大小.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com