
【題目】已知點![]() 在橢圓
在橢圓![]() :
:![]() (
(![]() )上,且點
)上,且點![]() 到左焦點
到左焦點![]() 的距離為3.
的距離為3.

(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 關于坐標原點
關于坐標原點![]() 的對稱點為
的對稱點為![]() ,又
,又![]()
![]() 兩點在橢圓
兩點在橢圓![]() 上,且
上,且![]() ,求凸四邊形
,求凸四邊形![]() 面積的最大值.
面積的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由題意點![]() 到左焦點
到左焦點![]() 的距離為3,結合兩點間距離公式可求得
的距離為3,結合兩點間距離公式可求得![]() 的值,將點
的值,將點![]() 代入橢圓,根據橢圓中
代入橢圓,根據橢圓中![]() 的關系式即可求得
的關系式即可求得![]() ,進而得橢圓的標準方程.
,進而得橢圓的標準方程.
(2)由![]() 可設直線
可設直線![]() 的方程為
的方程為![]() ,聯立橢圓方程,整理變形根據兩個交點可令
,聯立橢圓方程,整理變形根據兩個交點可令![]() 求得
求得![]() 的范圍.設
的范圍.設![]()
![]() ,由韋達定理表示出
,由韋達定理表示出![]() ,
,![]() ,由弦長公式求得
,由弦長公式求得![]() ,點到直線距離公式求得
,點到直線距離公式求得![]() 到
到![]() 的距離,結合
的距離,結合![]() 用
用![]() 表示出
表示出![]() ,令
,令![]() ,可化簡為
,可化簡為![]() ,再令
,再令![]() ,利用導函數求得
,利用導函數求得![]() 的單調性和最值,即可求解.
的單調性和最值,即可求解.
(1)因為橢圓![]() 經過點
經過點![]() ,所以
,所以![]() .
.
設左焦點![]() (
(![]() ),
),
則由![]() 得
得![]() ,
,
解得![]() .
.
又![]() ,于是
,于是![]() ,
,
解得![]() (舍負),
(舍負),
進而![]() .
.
故橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)因為![]() ,可設直線
,可設直線![]() 的方程為
的方程為![]() (
(![]() ),
),
聯立 并整理得
并整理得![]() .
.
由![]() ,解得
,解得![]() .
.
設![]()
![]() ,則
,則![]() ,
,![]() .
.
所以![]()
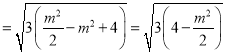 .
.
又![]() 與
與![]() 之間的距離即
之間的距離即![]() 到
到![]() 的距離
的距離![]() ,且
,且![]() .
.
所以四邊形![]() 的面積
的面積 .
.
設![]() ,由
,由![]() 可得
可得![]() ,
,
則![]() ,
,
記之為函數![]() ,則
,則![]() ,
,
易知![]() 在區間
在區間![]() 內單調遞增,在區間
內單調遞增,在區間![]() 內單調遞減.
內單調遞減.
故![]() 的最大值為
的最大值為![]() ,此時
,此時![]() ,解得
,解得![]() ,符合題意,
,符合題意,
所以四邊形![]() 面積的最大值為
面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:![]() )和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)作出使用了節水龍頭50天的日用水量數據的頻率分布直方圖;
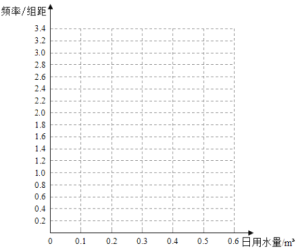
(2)估計該家庭使用節水龍頭后,日用水量小于0.3![]() 的概率;
的概率;
(3)估計該家庭用節水龍頭后,一年能節省多少水.(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取某廠的某種產品400件,經質檢,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生產1件一、二、三等品獲得的利潤分別為6萬元、2萬元、1萬元,而1件次品虧損2萬元.設1件產品的利潤(單位:萬元)為![]() .
.
(1)求![]() 的分布列和1件產品的平均利潤(即
的分布列和1件產品的平均利潤(即![]() 的期望);
的期望);
(2)經技術革新后,仍有四個等級的產品,但次品率降為1%,一等品率提高為70%.如果此時要求1件產品的平均利潤不小于4.75萬元,則三等品率最多是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某控制器中有一個易損部件,現統計了30個該部件的使用壽命,結果如下(單位:小時);
710 721 603 615 760 742 841 591 590 721 718 750 760 713 709
681 736 654 722 732 722 715 726 699 755 751 709 733 705 700
(1)估計該部件的使用壽命達到一個月及以上的概率(一個月按30天計算);
(2)為了保證該控制器能穩定工作,將若干個同樣的部件按下圖連接在一起組成集成塊,每一個部件是否能正常工作互不影響.對比![]() 和
和![]() 時,哪個能保證集成塊使用壽命達到一個月及以上的概率超過0.8?
時,哪個能保證集成塊使用壽命達到一個月及以上的概率超過0.8?
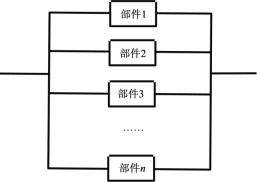
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為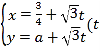 為參數
為參數![]() ,圓C的標準方程為
,圓C的標準方程為![]() 以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
![]() 求直線l和圓C的極坐標方程;
求直線l和圓C的極坐標方程;
![]() 若射線
若射線![]() 與l的交點為M,與圓C的交點為A,B,且點M恰好為線段AB的中點,求a的值.
與l的交點為M,與圓C的交點為A,B,且點M恰好為線段AB的中點,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年5月20日以來,廣東自西北到東南出現了一次明顯降雨.為了對某地的降雨情況進行統計,氣象部門對當地20日~28日9天內記錄了其中100小時的降雨情況,得到每小時降雨情況的頻率分布直方圖如下:
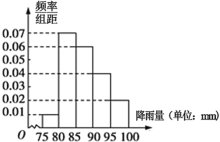
若根據往年防汛經驗,每小時降雨量在![]() 時,要保持二級警戒,每小時降雨量在
時,要保持二級警戒,每小時降雨量在![]() 時,要保持一級警戒.
時,要保持一級警戒.
(1)若以每組的中點代表該組數據值,求這100小時內每小時的平均降雨量;
(2)若從記錄的這100小時中按照警戒級別采用分層抽樣的方法抽取10小時進行深度分析.再從這10小時中隨機抽取3小時,求抽取的這3小時中屬于一級警戒時間的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com