
已知正項數列{an}中,a1=1,且log3an,log3an+1是方程x2 (2n
(2n 1)x+bn=0的兩個實根.
1)x+bn=0的兩個實根.
(1)求a2,b1;
(2)求數列{an}的通項公式;
(3)若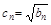 ,
,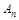 是
是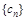 前
前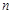 項和,
項和, 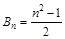 ,當
,當 時,試比較
時,試比較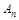 與
與 的大小.
的大小.
(1) ,
, ;(2)
;(2) ;(Ⅲ)當
;(Ⅲ)當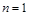 時,
時,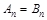 ,當
,當 時,
時, 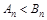 .
.
解析試題分析:(1) 是方程
是方程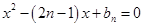 的兩個實根,有根與系數關系可得,
的兩個實根,有根與系數關系可得,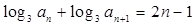 ,
, ,求
,求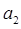 ,
,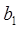 的值,可利用對數的運算性質,及已知
的值,可利用對數的運算性質,及已知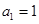 ,只需令
,只需令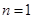 即可求出
即可求出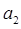 ,
,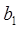 的值;(2)求數列
的值;(2)求數列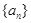 的通項公式,由
的通項公式,由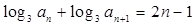 得,
得,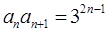 ,所以
,所以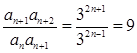 ,即
,即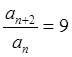 ,得數列
,得數列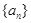 的奇數項和偶數項分別是公比為9的等比數列,分別寫出奇數項和偶數項的通項公式,從而可得數列
的奇數項和偶數項分別是公比為9的等比數列,分別寫出奇數項和偶數項的通項公式,從而可得數列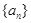 的通項公式;(Ⅲ)若
的通項公式;(Ⅲ)若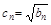 ,
,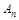 是
是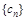 前
前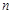 項和,
項和, 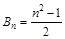 ,當
,當 時,試比較
時,試比較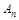 與
與 的大小,此題關鍵是求數列
的大小,此題關鍵是求數列 的通項公式,由(1)可知
的通項公式,由(1)可知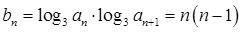 ,可得
,可得 ,當
,當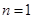 時,
時, 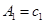 =0,
=0,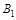 =0,得
=0,得 ,當
,當 時,有基本不等式可得
時,有基本不等式可得 ,從而可得
,從而可得 0+
0+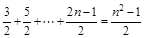 =
= ,即可得結論.
,即可得結論.
試題解析:(1) ,
,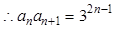
當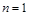 時,
時,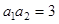 ,
,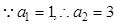 ,
, ,
,
(2)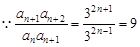 ,
,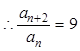 ,
,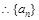 的奇數項和偶數項分別是公比為9的等比數列.
的奇數項和偶數項分別是公比為9的等比數列.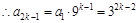 ,
,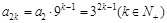 ,
,
(3) 
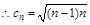
當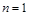 時,
時, 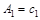 =0,
=0,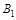 =0,
=0,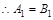 .
.
當 時,
時,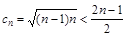
 0+
0+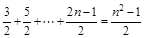 =
=
綜上,當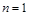 時,
時,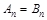 ,當
,當 時,
時, 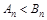 .
.
或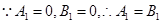


猜測 時,
時,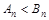 用數學歸納法證明
用數學歸納法證明
①當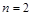 時,已證
時,已證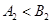
②假設 時,
時, 成立
成立
當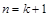 時,
時,

 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com