
【題目】設函數f(x)的定義域為R,f(x)= ![]() ,且對任意的x∈R都有f(x+1)=﹣
,且對任意的x∈R都有f(x+1)=﹣ ![]() ,若在區間[﹣5,1]上函數g(x)=f(x)﹣mx+m恰有5個不同零點,則實數m的取值范圍是( )
,若在區間[﹣5,1]上函數g(x)=f(x)﹣mx+m恰有5個不同零點,則實數m的取值范圍是( )
A.[﹣ ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0]
,0]
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
【題目】已知集合A={x|3≤3x≤27}, ![]() .
.
(1)分別求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期為π. (Ⅰ)當x∈[0,
)﹣1(ω>0),f(x)的最小正周期為π. (Ⅰ)當x∈[0, ![]() ]時,求f(x)的最大值;
]時,求f(x)的最大值;
(Ⅱ)請用“五點作圖法”畫出f(x)在[0,π]上的圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有長分別為1m、2m、3m的鋼管各3根(每根鋼管質地均勻、粗細相同附有不同的編號),從中隨機抽取2根(假設各鋼管被抽取的可能性是均等的),再將抽取的鋼管相接焊成筆直的一根.若X表示新焊成的鋼管的長度(焊接誤差不計).
(1)求X的分布列;
(2)若Y=﹣λ2X+λ+1,E(Y)>1,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
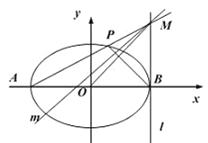
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的焦距為2,且過點
的焦距為2,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 分別是橢圓
分別是橢圓![]() 的左右頂點,直線
的左右頂點,直線![]() 經過點
經過點![]() 且垂直與軸,點
且垂直與軸,點![]() 是橢圓上異于
是橢圓上異于![]() 的任意一點,直線
的任意一點,直線![]() 交
交![]() 于點
于點![]() .
.
①設直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:
,求證:![]() 為定值;
為定值;
②設過點![]() 垂直于
垂直于![]() 的直線為
的直線為![]() ,求證:直線
,求證:直線![]() 過定點,并求出定點的坐標.
過定點,并求出定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+(y﹣1)2=5,直線l:mx﹣y+1﹣m=0. (Ⅰ)求證:對m∈R,直線l與圓C總有兩個不同交點;
(Ⅱ)設l與圓C交與不同兩點A、B,求弦AB的中點M的軌跡方程;
(Ⅲ)若定點P(1,1)分弦AB為 ![]() =
= ![]() ,求此時直線l的方程.
,求此時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 若對任意的正整數n,總存在正整數m,使得Sn=am , 則稱{an}是“H數列”.
(1)若數列{an}的前n項和為Sn=2n(n∈N*),證明:{an}是“H數列”;
(2)設{an}是等差數列,其首項a1=1,公差d<0,若{an}是“H數列”,求d的值;
(3)證明:對任意的等差數列{an},總存在兩個“H數列”{bn}和{cn},使得an=bn+cn(n∈N*)成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com