
【題目】已知F是拋物線y2=4x的焦點,點A,B在該拋物線上且位于x軸的兩側(cè),OA⊥OB(其中O為坐標原點),則△AOB與△AOF面積之和的最小值是( )
A.16
B.8![]()
C.8![]()
D.18
【答案】C
【解析】解:設直線AB的方程為:x=ty+m,
點A(x1 , y1),B(x2 , y2),直線AB與x軸的交點為M(m,0),
x=ty+m代入y2=4x,可得y2﹣4ty﹣4m=0,
根據(jù)韋達定理有y1y2=﹣4m,
∵OA⊥OB,
∴![]()
![]() =0,
=0,
∴x1x2+y1y2=0,從而(![]() y1
y1![]() y2)2+y1y2=0,
y2)2+y1y2=0,
∵點A,B位于x軸的兩側(cè),
∴y1y2=﹣16,故m=4.
不妨令點A在x軸上方,則y1>0,
又F(1,0),
∴S△ABO+S△AFO=![]() ×4×(y1﹣y2)+
×4×(y1﹣y2)+![]() ×y1=
×y1=![]() y1+
y1+![]()
≥8![]() ,
,
當且僅當![]() y1=
y1=![]() , 即y1=
, 即y1=![]() 時,取“=”號,
時,取“=”號,
∴△ABO與△AFO面積之和的最小值是8![]() ,
,
故選:C.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業(yè)本系列答案
新思維小冠軍100分作業(yè)本系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在正方體ABCDA1B1C1D1中,O為底面ABCD的中心,P,Q分別為![]() 的中點.
的中點.
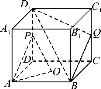
求證:(1)平面D1 BQ∥平面PAO.
(2)求異面直線QD1與AO所成角的余弦值;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若![]() 則一定有( )
則一定有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】本題主要考查不等關系。已知![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 。故選
。故選![]()
【題型】單選題
【結(jié)束】
5
【題目】關于x的不等式ax2+bx+2>0的解集為{x|-1<x<2},則關于x的不等式bx2-ax-2>0的解集為( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設B、C是定點,且均不在平面α上,動點A在平面α上,且sin∠ABC=![]() , 則點A的軌跡為( )
, 則點A的軌跡為( )
A.圓或橢圓
B.拋物線或雙曲線
C.橢圓或雙曲線
D.以上均有可能
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知等比數(shù)列{an}、等差數(shù)列{bn},滿足a1>0,b1=a1﹣1,b2=a2 , b3=a3且數(shù)列{an}唯一.
(1)求數(shù)列{an},{bn}的通項公式;
(2)求數(shù)列{anbn}的前n項和.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}滿足a1=1,an+1=2an+1.
(1)求數(shù)列{an}的通項公式;
(2)令bn=![]() n(an+1),求數(shù)列{bn}的前n項和Tn .
n(an+1),求數(shù)列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,求點D的坐標;
,求點D的坐標;
(2)問是否存在實數(shù)α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,說明理由.
成立?若存在,求出α,β的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分12分)
如圖1,在Rt![]() 中,
中,![]() ,
,![]() .D、E分別是
.D、E分別是![]() 上的點,且
上的點,且![]() ,將
,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如圖2.
,如圖2.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 與平面
與平面![]() 所成角的余弦值;
所成角的余弦值;
(Ⅲ)當![]() 點在何處時,
點在何處時,![]() 的長度最小,并求出最小值.
的長度最小,并求出最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義在R上的奇函數(shù)f(x)滿足f(x+1)=f(﹣x),當x∈(0,1)時,f(x)=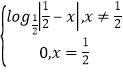 , 則f(x)在區(qū)間(1,
, 則f(x)在區(qū)間(1,![]() )內(nèi)是( )
)內(nèi)是( )
A.增函數(shù)且f(x)>0
B.增函數(shù)且f(x)<0
C.減函數(shù)且f(x)>0
D.減函數(shù)且f(x)<0
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com